Methyltin chloride

Using object cloning, multiple data sets, and multiple k-weights

This example will deomnstrate several features of DEMETER, including object cloning, multiple data set fitting, and multiple k-weights in a fit. The data are dimethyl tin dichloride and monomethyl tin trichloride, both in solution. These organic tin compounds consist of a tin atom surrounded tetrahedrally by chlorine atoms and methyl (CH₃) groups.

Obviously, this is not a crystal. To start, I found structural information for the dimethyltin molecule in the form of a Protein Databank File. This is shown here:

COMPND    5261536
HETATM    1  C1  LIG     1      -0.027   2.146   0.014  1.00  0.00
HETATM    2 SN2  LIG     1       0.002  -0.004   0.002  1.00  0.00
HETATM    3  C3  LIG     1       1.042  -0.716   1.744  1.00  0.00
HETATM    4 CL4  LIG     1      -2.212  -0.821   0.019  1.00  0.00
HETATM    5 CL5  LIG     1       1.107  -0.765  -1.940  1.00  0.00
HETATM    6 1H1  LIG     1       0.996   2.523   0.006  1.00  0.00
HETATM    7 2H1  LIG     1      -0.554   2.507  -0.869  1.00  0.00
HETATM    8 3H1  LIG     1      -0.537   2.497   0.911  1.00  0.00
HETATM    9 1H3  LIG     1       0.532  -0.365   2.641  1.00  0.00
HETATM   10 2H3  LIG     1       1.057  -1.806   1.738  1.00  0.00
HETATM   11 3H3  LIG     1       2.065  -0.339   1.736  1.00  0.00
END

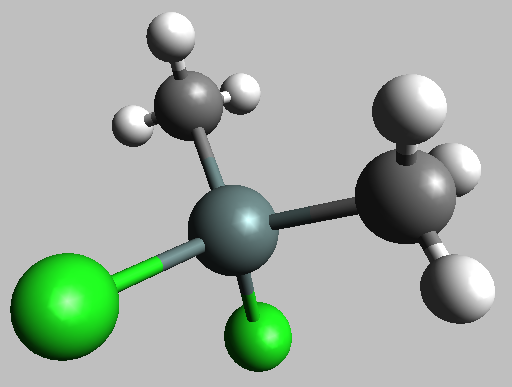
This structure is shown here as a ball-and-stick figure. The monomethyl tin looks just like this, except that one of the methyl groups is replaced by another chlorine atoms.

This is simply converted to a feff.inp file by cutting and pasting the atomic coordinates and lfleshing out the input file with a potentials list and FEFF boilerplate. Note that the central atom need not be at (0,0,0) nor does it need to be the first item in the atoms list. To constrain the muffin tin potentials abd assure physically reasonable muffin tin radii, it might be prudent to insert a shell of waters around the molecule. Without some theoretical (molecular dynamics, for instance) help, doing so would be pretty ad hoc. Not doing so is certainly the simplest way to proceed, so let's do that. The feff.inp is shown here:

 TITLE dimethyltin dichloride

 HOLE 1   1.0 

 *         mphase,mpath,mfeff,mchi
 CONTROL   1      1     1     1
 PRINT     1      0     0     0

 RMAX        6.0
 NLEG         4

 POTENTIALS
 *    ipot   Z  element
        0   50   Sn        
        1   17   Cl
        2    6   C
        3    1   H

 ATOMS
 *   x          y          z  
   -0.027   2.146   0.014  2
    0.002  -0.004   0.002  0
    1.042  -0.716   1.744  2
   -2.212  -0.821   0.019  1
    1.107  -0.765  -1.940  1
    0.996   2.523   0.006  3
   -0.554   2.507  -0.869  3
   -0.537   2.497   0.911  3
    0.532  -0.365   2.641  3
    1.057  -1.806   1.738  3
    2.065  -0.339   1.736  3

Armed with a feff.inp file, we are ready to proceed with the fit.

#!/usr/bin/perl
use Demeter qw(:ui=screen :plotwith=gnuplot);

## -------- Import data from a project file
my $prj = Demeter::Data::Prj->new(file=>'methyltin.prj');
my @common = (fft_kmin => 2, fft_kmax => 10.5,
              bft_rmin => 1, bft_rmax => 2.4,
              fit_k1   => 1, fit_k2   => 1,    fit_k3 => 1);
my $mmt = $prj->record(1);
$mmt -> set(name => "Monomethyltin trichloride", @common);
my $dmt = $prj->record(2);
$dmt -> set(name => "Dimethyltin dichloride", @common);

## -------- make a Feff calculation
my $feff = Demeter::Feff->new(file=>'methyltin.inp');
$feff -> set(workspace=>'feff', screen=>0);
$feff -> make_workspace;
$feff -> run;
my @list = $feff -> list_of_paths;

## -------- make some guess parameters
my @gds = (Demeter::GDS->new(name=>'amp',     gds=>'guess', mathexp=>1),
           Demeter::GDS->new(name=>'enot',    gds=>'guess', mathexp=>0),
           Demeter::GDS->new(name=>'delr_c',  gds=>'guess', mathexp=>0),
           Demeter::GDS->new(name=>'ss_c',    gds=>'guess', mathexp=>0.003),
           Demeter::GDS->new(name=>'delr_cl', gds=>'guess', mathexp=>0),
           Demeter::GDS->new(name=>'ss_cl',   gds=>'guess', mathexp=>0.003),
          );

## -------- define some paths
my @paths = (Demeter::Path->new(name    => "carbon neighbor",
                                sp      => $list[0],
                                parent  => $feff,
                                data    => $dmt,
                                n       => 2,
                                s02     => 'amp',
                                e0      => 'enot',
                                delr    => 'delr_c',
                                sigma2  => 'ss_c',),
             Demeter::Path->new(name    => "chlorine neighbor",
                                sp      => $list[1],
                                parent  => $feff,
                                data    => $dmt,
                                n       => 2,
                                s02     => 'amp',
                                e0      => 'enot',
                                delr    => 'delr_cl',
                                sigma2  => 'ss_cl',)
            );
push @paths, $paths[0]->Clone(n=>1, data=>$mmt);
push @paths, $paths[1]->Clone(n=>3, data=>$mmt);

## -------- and fit!
my $fit = Demeter::Fit->new(data  => [$dmt, $mmt],
                            paths => \@paths,
                            gds   => \@gds);
$fit -> fit;
$fit -> interview;

The data on the two methyltin molecules is imported from an ATHENA project file at lines 5-12. The FEFF calculation is made at lines 15-18 and the list of ScatteringPath objects is imported at line 19 using the list_of_path method, which is a convenience method which returns a list rather than a reference to a list. The ScatteringPath object representing scattering from the carboin atom in the methyl group is the first item in this list, the ScatteringPath for the chlorine atom is the second item in this list.

At lines 31-49, these two paths are parameterized and assigned to the dimethyl tin data. At lines 50 and 51, these two paths are cloned and assigned to the monomethyl tin data. The n attributes of the two cloned paths are set to 1 and 4 -- appropriate for the monomethyl tin trichloride.

This is a fairly simple fitting model that assumes that the tin-carbon and tin-chlorine bonds behave identically for each molecule. This simple assumption is made by changing the n attributes of the cloned paths, but not any of the other path parameters. Of course, new GDS parameters could be introduced to the fit to lift this constraint and explore that assumption.

Finally, note that all three values for the fitting k-weights are used. This is indicated at line 8 then applied to both Data objects at lines 10 and 12. Doing a multiple k-weight fit is really that easy.

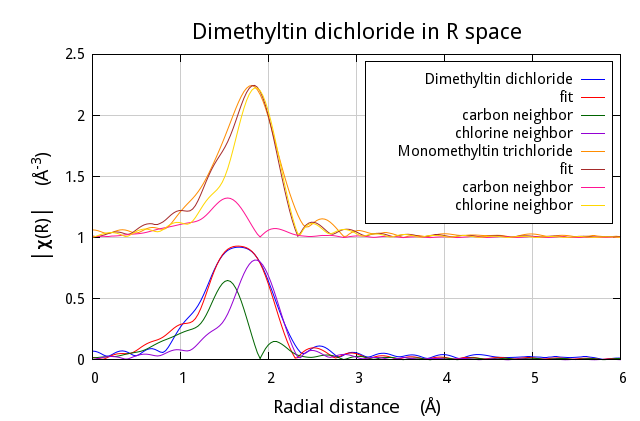
The lines below replaced the interview method to produce this plot of the result of the fit. Note the Data and Path objects are conveniently wrapped up in a foreach loop. The plotting syntax is transparent for these two object types and the Path objects use the y_offset attribute of the associated Data object. This is one of the reasons why every Path must have an associated Data object.   $fit-> po -> set(plot_fit =>  1,                    r_pl     => 'm',                    kweight  =>  2);   $mmt-> y_offset(1.0);   $_  -> plot('r') foreach ($dmt, @paths[0,1],                             $mmt, @paths[2,3]);   $mmt-> pause;

As a final note, I want to comment on lines 32 and 41 where the sp attribute of the Path objects is set to the proper ScatteringPath objects from the FEFF calculation. Choosing the correct ScatteringPaths from @list requires having specific knowledge of the order of the paths from the FEFF's pathfinder. That is not difficult to obtain using the intrp method of the Feff object, however it is something that is difficult to put in-line in a script like this. Of course, in this case, it is fairly obvious that the first two paths are the C and Cl single scattering paths. In general, though, it is hard to know a priori the order of paths that come from the pathfinder.

Semantic path descriptions are the solution to this problem. In this case, the find_path method of the Feff object could be used like so:

  $paths[0] -> set(sp => $feff->find_path(tag=>['C']);
  $paths[1] -> set(sp => $feff->find_path(tag=>['Cl']);

The find_path method can be relied upon to find the correct path regardless of the order of things after the pathfinder has done its work.