Example 1: FeS2

Introduction, blah blah, known crystal structure, blah blah, learn the mechanics of the program, blah blah

---

 

Import data

After starting ARTEMIS, click on the “Add” button at the top of the “Data sets” list in the Main window. This will open a file selection dialog. Click to find the ATHENA project file containing the data you want to analyze. Opening that project file displays the project selection dialog.

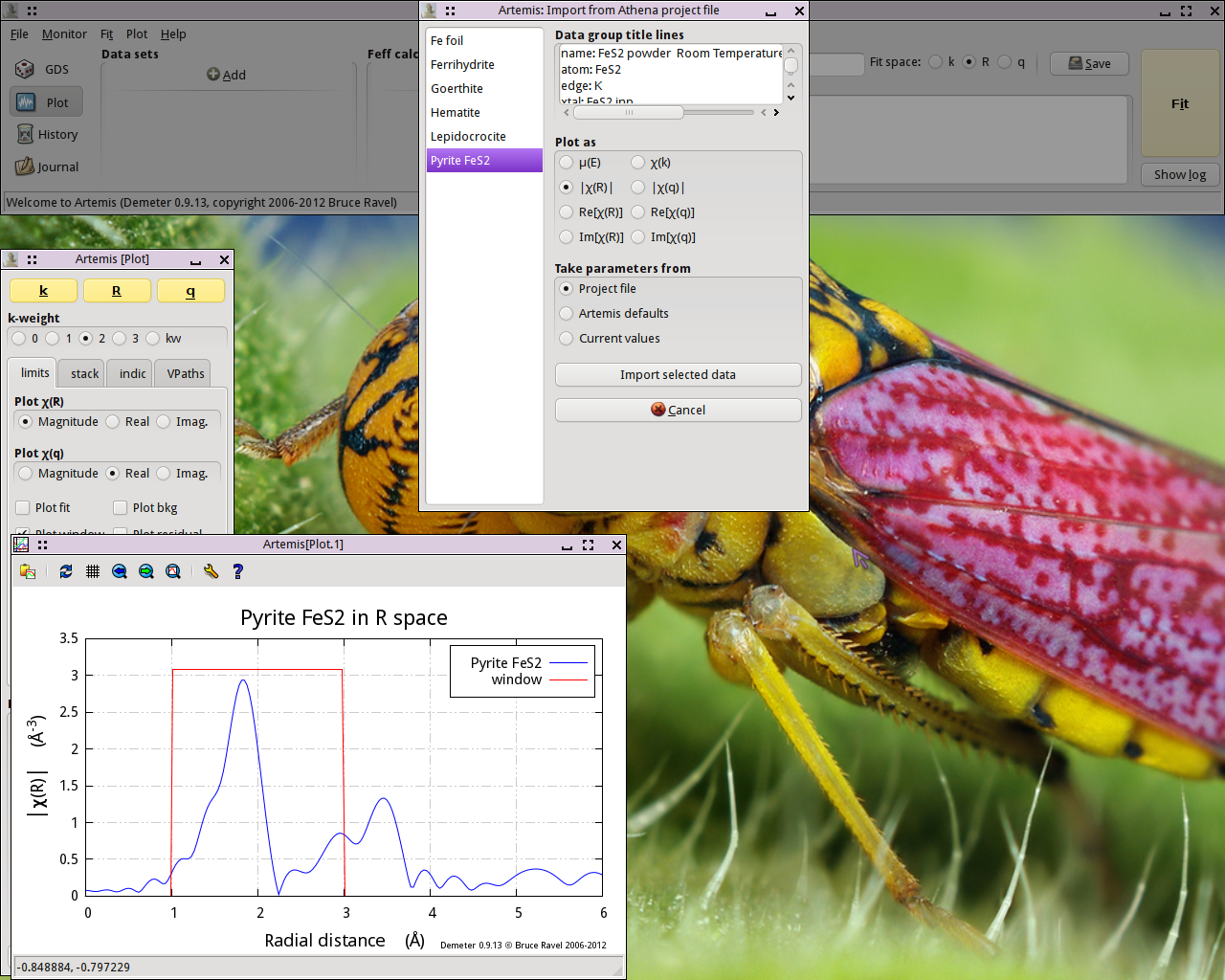
The project file used here has several iron standards. Select FeS₂ from the list. That data set gets plotted when selected.

Now click the “Import” button. That data set gets imported into ARTEMIS. An entry for the FeS₂ is created in the Data list, a window for interacting with the FeS₂ data is created, and the FeS₂ data are plotted as χ(k).

The next step is to prepare for the FEFF calculation using the known FeS₂ crystal structure. Clicking on the line in the Data window that says “Import crystal data or a Feff calculation” will post a file selection ddialog. Click to find the atoms.inp file containing the FeS₂ crystal structure.

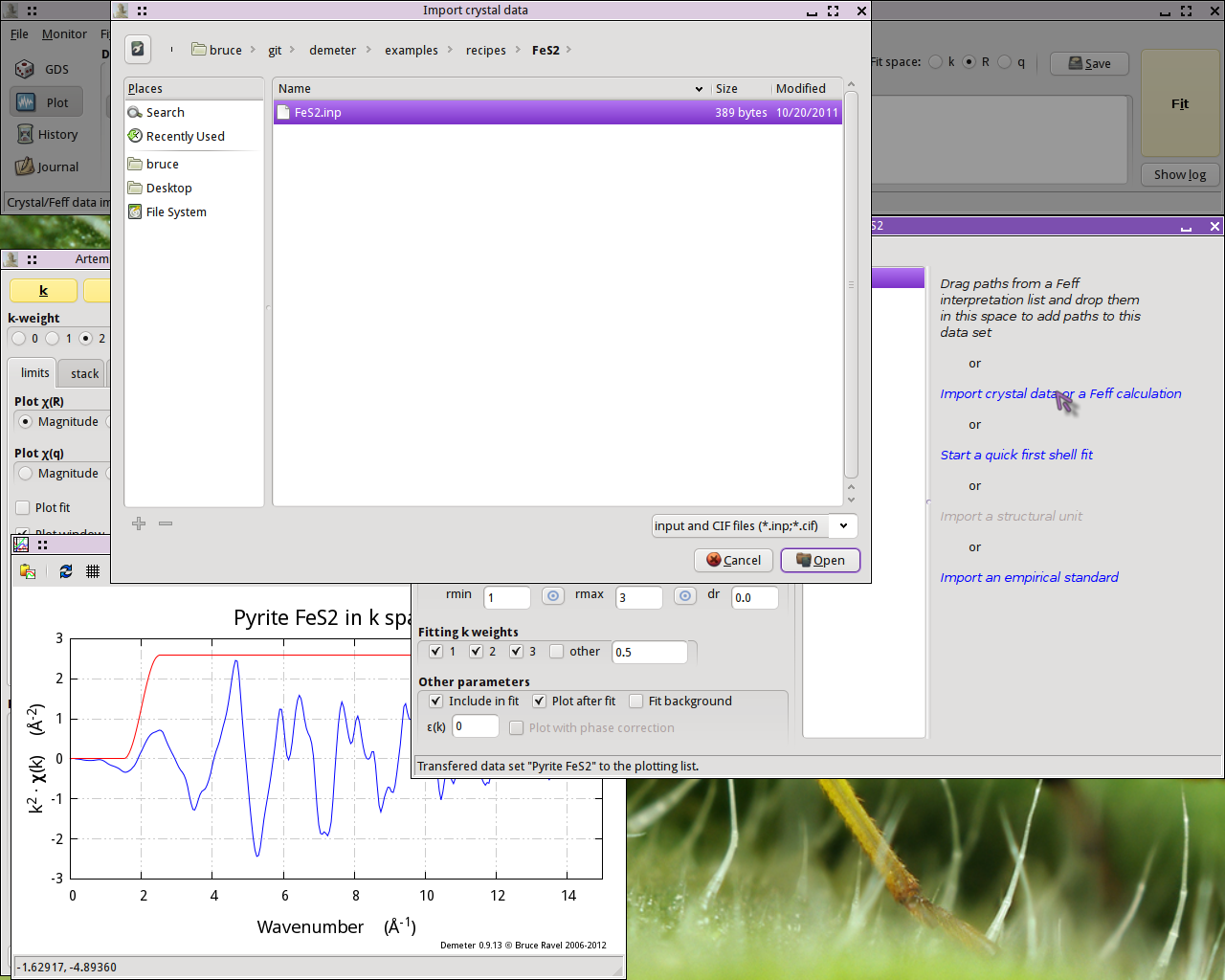
With the FeS₂ crystal data imported, run ATOMS by clicking the “Run Atoms” button on the Atoms tab of the FEFF windows. That will display the Feff tab containing the FEFF input data. Click the “Run Feff” button to compute the scattering potentials and to run the pathfinder.

Once the FEFF calculation is finished, the path intepretation list is shown in the Paths tab. This is the list of scattering paths, sorted by increasing path length. Select the first 11 paths by clicking on the path 0000, then shift-clicking on path 0010. These group of selected paths will be highlighted. Click on one of the highlighted paths and, without letting go of the mouse button, drag the paths over to the Data winodw. Drop the paths on the empty Path list.

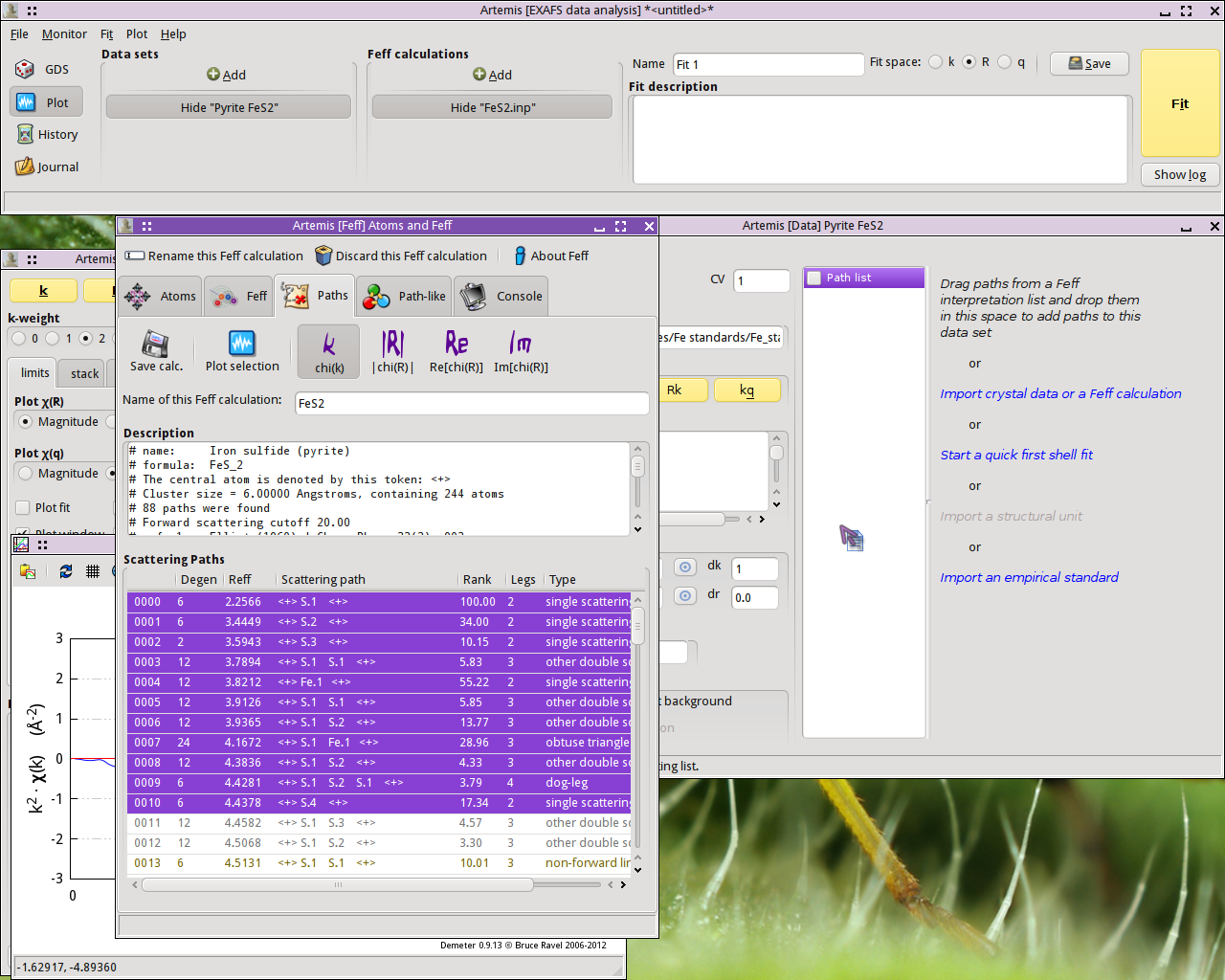
Dropping the paths on the Path list will associate those paths with that data set. That is, that group of paths is now available to be used in the fitting model for understanding the FeS₂ data.

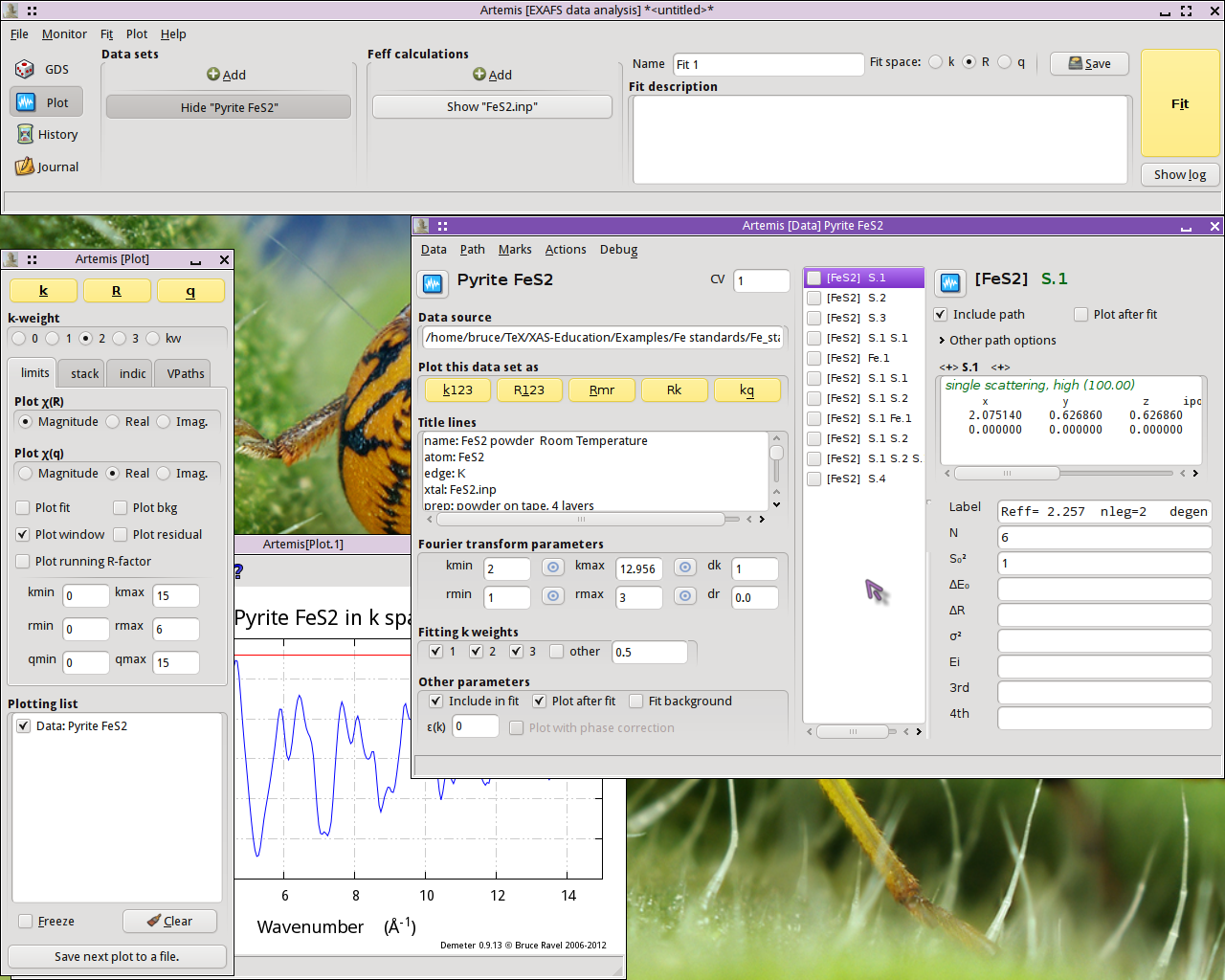
Each path will get its own Path page. The Path page for a path is displayed when that path is clicked upon in the Path list. Shown below is the FeS₂ data with its 11 paths. The first path in the list, the one representing the contribution to the EXAFS from the S single scattering path at 2.257 Å, is currently displayed.

---

 

Examine the scattering paths

The first chore is to understand how the various paths from the FEFF calculation relate to the data. To this end, we need to populate the Plotting list with data and paths and make some plots.

First let's examine how the single scattering paths relate to the data. Mark each of the first four single scattring paths – the ones labeled “S.1”, “S.2”, “S.3”, and “Fe.1” – by clicking on their check buttons. Transfer those four paths to the Plotting list by selecting “Transfer marked” from the Actions menu.

With the Plotting list poluated as shown below, click on the “R” plot button in the Plot window to make the plot shown.

The first interesting thing to note is that the first peak in the data seems to be entirely explained by the path from the S atom at 2.257 Å. None of the other single scattering paths contribute significantly to the region of R-space.

The second interesting thing to note is that the next three single scattering paths are not so well separated from one another. While it may be tempting to point at the peaks at 2.93 Å and 3.45 Å and assert that they are due to the second shell S and the fourth shell Fe, it is already clear that the situation is more complicated. Those three single scattering paths overlap one another. Each contriobutes at least some spectral weight to both of the peaks at 2.93 Å and 3.45 Å.

The first peak shold be reather simple to interpret, but higher shells are some kind of superposition of many paths.

What about the multiple scattering paths?

To examine those, first clear the Plotting list by clicking the “Clear” button at the bottom of the Plot window. Transfer the FeS₂ data back to the Plotting list by clicking its transfer button, . Mark the first three multiple scattering paths by clicking their mark buttons. Select “Transfer marked” from the Actions menu.

With the Plotting list newly populated, make a new plot of |χ(R)|.

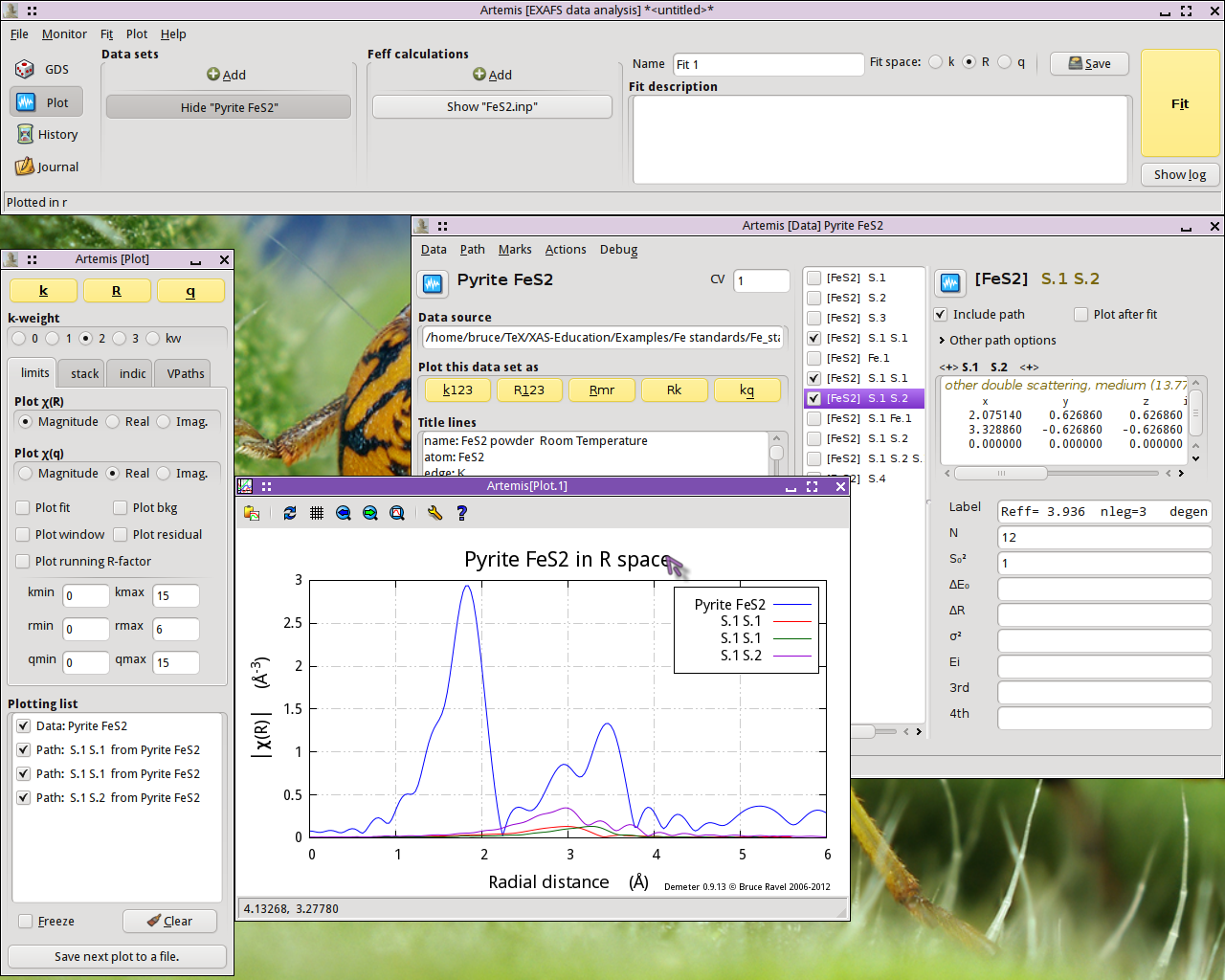
The two paths labeled “S.1 S.1”, which represent two different ways for the photoelectron to scatter from a S atom in the first coordination shell then scatter from another S atom in the first coordination shell, contribute rather little spectra weight. Given their small size, it seems possible that we may be able to ignore those paths when we analyze our FeS₂ data.

The “S.1 S.2” path, which first scatters from a S in the first coordination shell then from a S in the second coordination shell, contributes significantly to the peak at 2.93 Å. It seems unlikely that we will be able to ignore that path.

To examine the next three multiple scattering paths, clear the Plotting l ist, mark those paths, and repopulate the Plotting lilst.

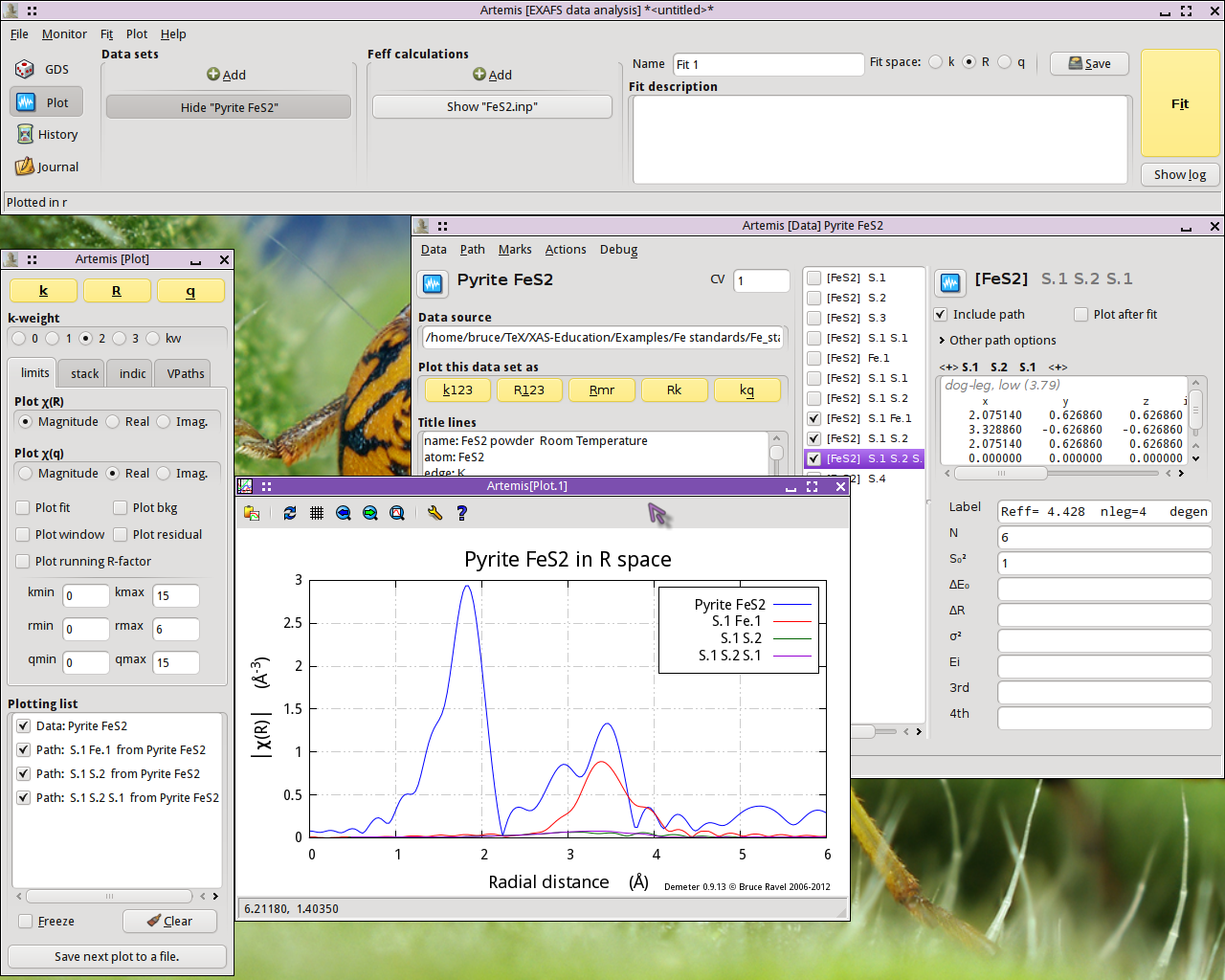
The “S.1 Fe.1” path, which scatters from a S atom in the first coordination shell then scatters from an Fe atom in the fourth coordination shell, is quite substantial. It will certainly need to be considered in our fit. The other two paths are tiny.

---

 

Fit to the first coordination shell

We begin by doing an analysis of the first shell. As we saw above, we only need the first path in the path list. To prepare for the fit, we do the following:

1. Exclude all but the first path from the fit. With the first path selected in the path list and displayed, select “Mark after current” from the Marks menu. This will mark all paths except for the first one. Then select “Exclude marked” from the Actions menu. This will exclude those paths from the fit. That is indicated by the triple parentheses in the path list.

2. Set the values of R_min and R_max to cover just the first peak.

3. For this simple first shell fit, we set up a simple, four-parameter model. The parameters amp, enot, delr, and ss are defined in the GDS window and given sensible initial guess values.

4. The path parameters for the first shell path are set. S²₀ is set to amp, E₀ is set to enot, ΔR is set to delr, and σ² is set to ss.

Note that the current settings for k- and R-range result in a bit more than 7 independent points, as computed from the Nyquist criterion. With only 4 guess parameters, this should be a reasonable fitting model.

Now hit the “Fit” button. Upon completion of the fit, the following things happen:

1. An Rmr plot is made of the data and the fit.

2. The log Window is displayed with the results of the fit

3. The Fit and plot buttons are recolored according to the evaluation of the happiness parameter.

4. The Plotting list is cleared and repopulated with the data.

5. The fit is entered into the History window (which is not in the screenshot below).

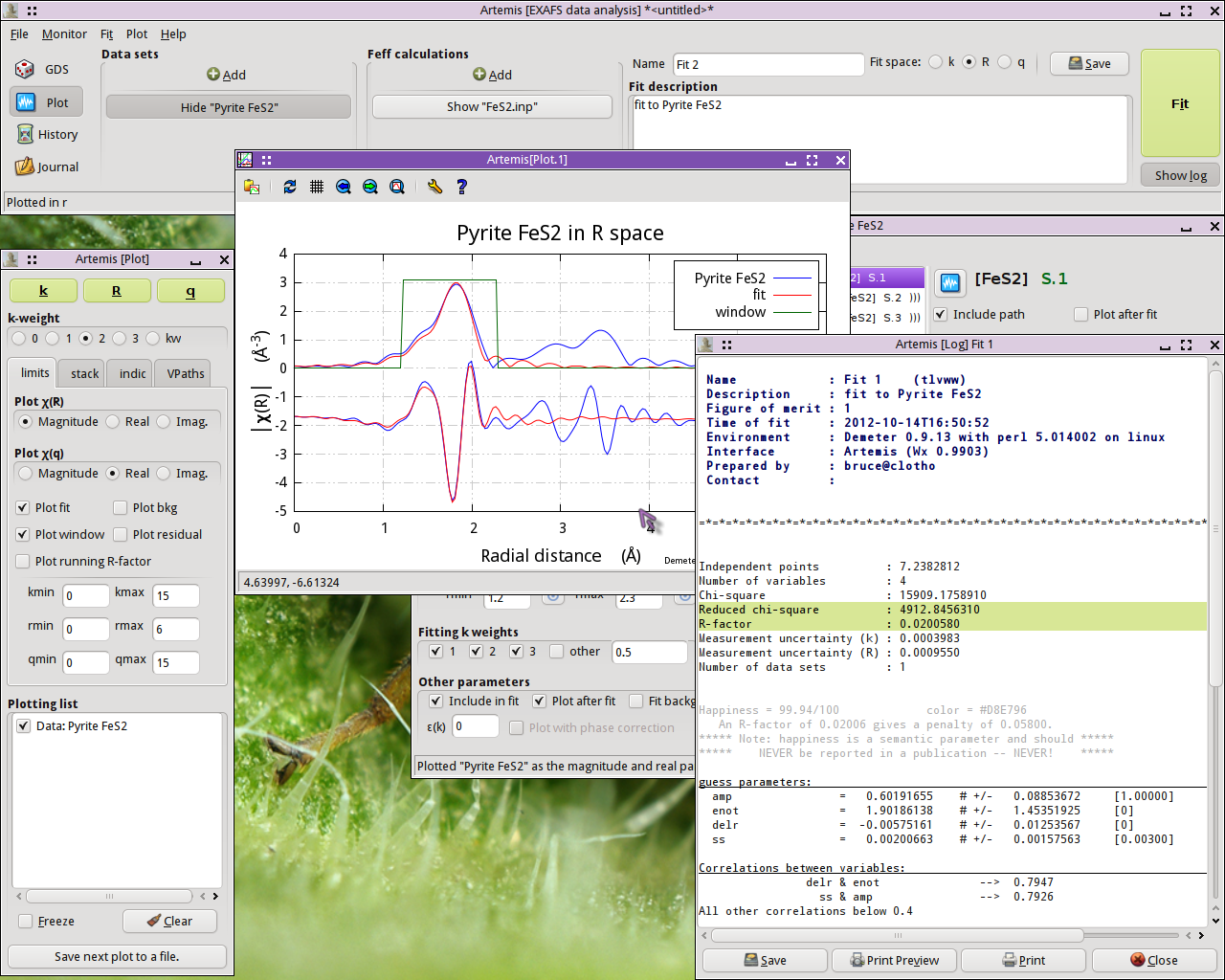
This is not a bad result. The value of enot is small, indicatng that a reasonable value of E₀ was chosen back in ATHENA. delr is small and consistent with 0, as we should expect for a known crystal. ss is a reasonable value with a reasonable error bar. The only confusing parameter is amp, which is a bit smaller than we might expect for a S²₀ value.

The correlations between parameters are of a size that we expect. The R-factor evaluates to about 2% misfit. χ²_ν is really huge, but that likely means that ε was not evaluated correctly. All in all, this is a reasonable fit.

---

 

Extending the fit to higher shells

---

 

The final fitting model

---

 

Additional questions