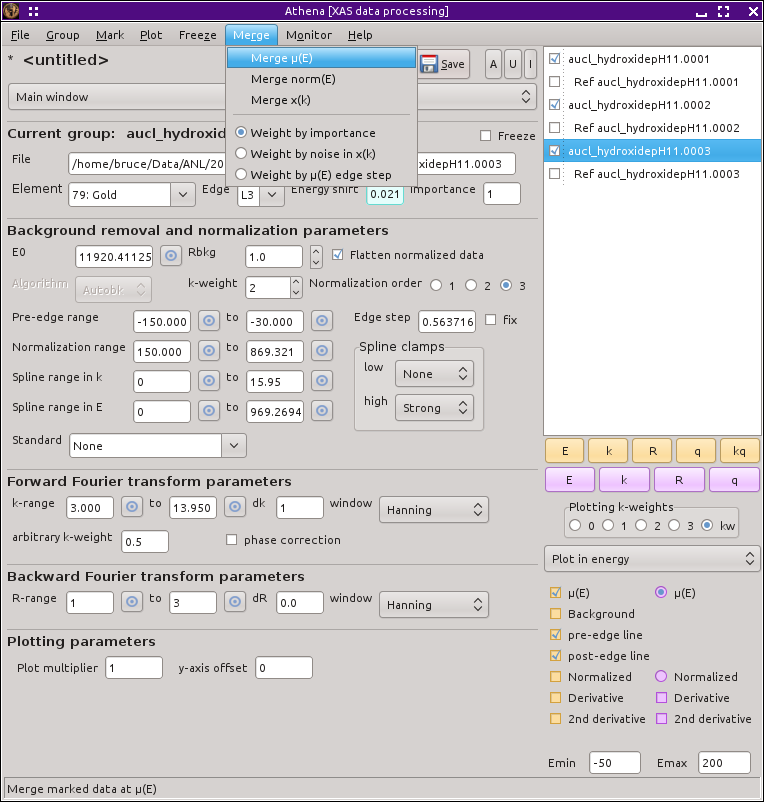
Merging data groups

Averaging scans and computing their standard deviation

Sadly, most data that we measure is, frankly, kind of crappy. A single scan typically ranges from noisy to so dominated by noise that it's hard to recognize it as oscillatory. Fortunately, the central limit theorem works every single time. If you add up enough noisy scans, it eventually turns into real data!

All entries in the group list which are marked will be included in the merge. Make sure that the marked groups really are the ones you want to include in the merge!

Data can be merged as μ(E), normalized μ(E), or χ(k). In most cases, it makes little difference which one you choose. χ(R) will be the same regardless. (This can be tested, in fact, I encourage you to do so.) The standard deviation in the merged data is also computed and stays with the data in project and certain output files, although ATHENA does nothing else with the standard deviation other than plotting it, which is shown below. By default, each data set is weighted the same in the merge.

The contents of the Merge menu, showing the various ways that data can merged.

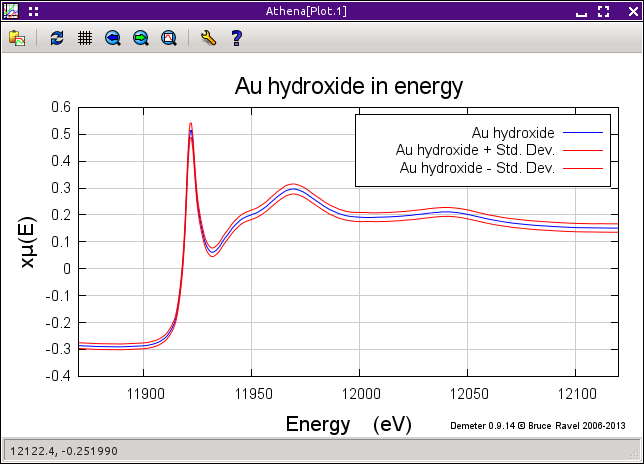
After a merge is made, a plot is displayed showing the merge in some manner. The type of merge plot is controled by the ♦Athena → merge_plot configuration parameter. The default is to show the data along with the data ± the standard devaition, as shown below. The other options are the the variance plot or a plot with the merge and all the data that entered the merge.

Data merged as μ(E) plotted with its standard deviation.

The data merging feature is one of ATHENA's most important. My typical work pattern is to carefully align the scans measured on a sample, merge them, then further work with the merged data in ATHENA and ARTEMIS.

It is essential that your data be well-aligned before merging. Merging poorly aligned data has the effect of significantly attenuating the fine structure.

When merging as μ(E) or normalized μ(E), if every data group included in the merge has a reference channel, the reference channels will also be merged and these two merged spectra will be tied together as a reference channels. Thus the merge of the reference channels can serve as the alignment standard for the merge of the data.

There is one situation where merging as μ(E) will be substantively different from the other two options. If something happens to change the values of the signals on the detectors in such a way that μ(E) for subsequent scans is of very different sizes but the normalized μ(E) data is consistent for all the data, then the merge in μ(E) will be dominated by the scans with larger absolute values while the merge in normalized μ(E) will treat all the data with similar weights. One way of having this happen is to change amplifier gains between scans. In that situation, you probably should choose to merge normalized or χ(k) data.

Merging options

Weighting options

There are three ways to weight the spectra which go into the merge. The default is to merge by the value of the «importance» parameter. Since the «importance» is by default 1, this choice usually means to weight the spectra equally in the merge. Because «importance» is a user-definable parameter, the weighting can be made in any way by setting those values appropriately. The other two options are attempts to weight according to quality of data. The “noise” option uses IFEFFIT's measure of noise in χ(k), thus giving more weight to data with less shot noise. The “edge step” uses the value of «edge step» determined form the normalization, thus giving more weight to data with larger edge steps. The idea for the edge step option is that, for data measured in fluorescence, a more concentrated sample has a larger edge step and is likely to give higher quality data. The choice between the three weighting options is made using the radio buttons in the Merge menu.

Preferences

There are preferences which have some influence on how the merge happens. ♦Merge → exclude_short_data allows you to choose whether to exclude data sets with far fewer data points into the merge. The default to exclude short data sets. ♦Merge → short_data_margin defines how many fewer data points triggers that exclusion for a data set. ♦Merge → weightby sets the default choice of weighting option between the three options explained above.

Keyboard shortcuts

There are keyboard shortcuts for merging:

• Control-shift-m : merge as μ(E)

• Control-shift-n : merge as normalized μ(E)

• Control-shift-c : merge as χ(k)