15.3. Geometric parametrization of bond length

15.3.1. Volumetric expansion coefficient

FeS₂ is a cubic crystal. Here is the crystal data

title name:     Iron sulfide (pyrite)
title formula:  FeS_2
title refer1:   Elliot (1960) J.Chem. Phys. 33(3), 903.
space  P a 3
a    = 5.404
rmax = 9.00     rpath = 6.00
core = Fe
atoms
  Fe     0.00000   0.00000   0.00000  Fe
  S      0.38400   0.38400   0.38400  S

In this case, there are only two parameters that determine the locations of all the atoms in the cluster – the lattice constant a and the position of the S atom in the unit cell. For now, we'll neglect the effect of the position of the S atom.

In the FeS2 worked example, a parameterization was used which related ΔR for all the paths to a volumetric expansion coefficient, ΔR= α · R_eff. Why does this work?

The distance d_eff between any two atoms in a cubic crystal is some geometrical factor multiplied by the lattice constant. That factor depends on the positions of the atoms in the unit cell, but is a pure number.

Thus, from the FEFF calculation, d_eff(i, j) = c_i,j· a₀ for any two atoms i and j. For any two pairs of atoms, c_i,j is a different number, but the distances between all pairs of atoms are related by simple geometry and the value of the lattice constant.

We consider an isotropic expansion (or contraction, if α is negative) of the unit, which is reasonable for a cubic lattice that does not undergo a phase transition. So a = (1 + α) · a₀.

The distance between any two atoms, after accounting for the isotropic expansion (or contraction) is

• d_i,j = d_eff(i,j) + Δd(i,j)
• d_i,j = c_i,j · a
• d_i,j = c_i,j · (1+ α ) · a₀
• d_i,j = c_i,j· a₀ + c_i,j· α · a₀
• ∴ Δd(i,j) = c_i,j· α · a₀
• and Δd(i,j) = α · d_eff(i,j)

The expression α · d_eff works for all legs of any SS or MS path in a cubic crystal (assuming that there are no internal degrees of freedom, like the parameter for the position of the S atom in FeS₂). The length of a path, then, is the sum of the length of each leg. ΔR for a path is the sum of Δd for each leg. The sum of the d_eff values is R_eff, thus ΔR= α · R_eff.

While this trick is only valid for a cubic crystal, it does ilustrate two important points about ARTEMIS. First, it is an example of an interesting math expression relating a path's ΔR value to a fitting parameter. The ΔR of the path is not itself a variable of the fit, rather it is written in terms of α, which is a variable of the fit.

Second, it is an example of a constraint which uses the information content of the data very well. We can include any number of paths with introducing new parameters for their ΔR values. α is a robust fitting parameter in the sense that every path is involved in its determination.

15.3.2. Propagating crystal distortion parameters

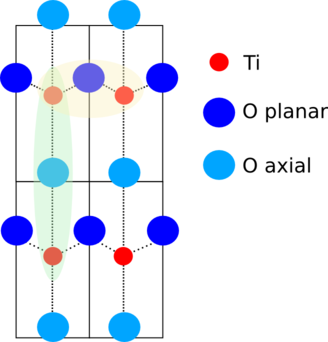
The room temperature structure of PbTiO₃ is a tetragonal modification of the perovskite structure. The c-axis is considerably longer than the a-axis. The Pb atoms lie at the corners of the tetragonal cell, the Ti atom lies near the center of the cell, and the O atoms lie near the centers of the faces.

In a setting which places the Pb atoms at positions of high symmetry, i.e. right on the cell corners, the other atoms are displaced from sites of symmetry c-direction. Here is the crystal data:

title PbTiO3 25C
title Glazer and Mabud, Acta Cryst. B34, 1065-1070 (1978)
core = ti    Space = P 4 m m
a = 3.905    c = 4.156
rmax=3.6
atoms
! At.type  x        y       z      tag
   Pb     0.0      0.0     0.0
   Ti     0.5      0.5     0.539
   O      0.5      0.5     0.1138  axial
   O      0.0      0.5     0.6169  planar

There are 5 parameters that determine the positions of all the atoms in the crystal, thus there are 5 parameters that determine the lengths of all scattering paths. They are the two lattice constants, the z-displacement of the Ti away from z=0, the z-displacement of the axial oxygen atom away from z=0.5, and the z-displacement of the planar oxygen atom away from z=0.5.

We set up a set of guess, def, and set parameters to encode this:

set   a0     = 3.905
guess dela   = 0
def   a      = a0 + dela

set   c0     = 4.156
guess delc   = 0
def   c      = c0 + delc

guess dti    = 0.039
guess doax   = 0.1138
guess dopl   = 0.1169

after volume = a*a*c

Fig. 15.14 Schematic of the displacement in PbTiO₃.

I have also defined an after parameter which computes the volume of the unit cell. While this will not serve a purpose in the fitting model, it is useful information to report to the log file.

A 2-dimensional cut through this distorted perovskite is shown to the right. The Pb atoms are above and below this plane, the axial oxygen atoms are in line with the titanium atoms. The planar oxygen atoms are in a slightly non-collinear, buckled alignment with the Ti atoms.

The distortions of the Ti and O atoms split the first coordination shell into three distance. Along the z-direction, there is a short Ti-O distance and long one. In the buckled plane, there are four equivalent Ti-O distances.

Computing these distances requires some simple geometry, with the planar distance being just a bit more complicated.

def    rtio_sh = (0.5 - (doax-dti)) * c
def    rtio_lo = (0.5 - (doax+dti)) * c

def    rtio_pl = sqrt( (a/2)^2 + ((dopl+dti)*c)^2 )

The second shell Pb atoms are similarly computed using trigonometry and the appropriate structural parameters.

def    rtipb_sh = sqrt( (a/2)^2 + c^2*(0.5 - dti)^2 )
def    rtipb_lo = sqrt( (a/2)^2 + c^2*(0.5 + dti)^2 )

Finally, the Ti-Ti distances in the thrid coordination shell are comparatively trivial. This shell is split by the tetragonal distortion into two subshells. The distances are the lattice constants, as you can be seen in the schematic above.

We now have math expressions for the interatomic distances between the Ti absorber and each type of scatterer up to the third coordination shell. These math expressions for these 7 paths are expressed in terms of the 5 guess parameters above. The nice thing about these expressions is that the interatomic distances are expressed in terms of easily intepretable parameters of the crystal structure.

Now, encoding the ΔR path parameter for each of these paths is simple. We just subtract R_eff from the corresponding math expression.

path short axial oxygen:
   delr = rtio_sh - reff

path planar oxygen:
   delr = rtio_pl - reff

path long axial oxygen:
   delr = rtio_lo - reff

path short lead:
   delr = rtipb_sh - reff

path long lead:
   delr = rtipb_lo - reff

path short titanium:
   delr = a - reff

path long titanium:
   delr = c - reff

There are important collinear or nearly-collinear multiple scattering paths at the distance of the third shell Ti atom. These are shown in the yellow and green shaded areas of the schematic above.

The ΔR parameters for the axial multiple scattering paths are simply the same as for the corresponding single scattering path. This is the case because the distortions in PbTiO₃ are all in the ẑ direction, so those MS paths must have the same length as the corresponding SS paths.

In the planar direction, you need to add up the lengths of the legs and subtract R_eff for their ΔR parameters:

path planar double scattering:
   delr = (a + 2*rtio_pl)/2  - reff

path planar triple scattering:
   delr = 2*rtio_pl - reff

This strategy of adding up leg lengths works for any kind of multiple scattering path you include in this fit.

This is lovely! With 5 guess parameters and some well-considered math expressions, we are able to encode ΔR parameters for all the paths in the fit. As more scattering paths are considered for the fit, it is not necessary to include any more guess parameters for ΔR.

15.3.3. Parametrizations of distance in non-crystalline materials

Interesting geometrical constraints on distance are not the sole province of crystalline materials. In the following two papers, I show the details of an analysis of Hg bound to the pyrimidine ring of a nucleotide in a synthetic DNA structure. To cope with severe information limits in my data, I made some simplifying assumptions about the structure of the Hg/DNA complex. I then employed a bit of trigonometry to express all the absorber-scatterer distances as functions of a small number of guess parameters.

• B Ravel. Composing complex EXAFS problems with severe information constraints. Journal of Physics: Conference Series, 190:012026, 2009. doi:10.1088/1742-6596/190/1/012026.
• B. Ravel, S. C. Slimmer, X. Meng, G. C. L. Wong, and Y. Lu. EXAFS studies of catalytic DNA sensors for mercury contamination of water. Radiation Physics and Chemistry, 78(10, Supplement):S75 – S79, 2009. doi:10.1016/j.radphyschem.2009.05.024.

Todo

Summarize parametrization from J Phys Conf Proc paper

---

DEMETER is copyright © 2009-2016 Bruce Ravel – This document is copyright © 2016 Bruce Ravel

This document is licensed under The Creative Commons Attribution-ShareAlike License.

If DEMETER and this document are useful to you, please consider supporting The Creative Commons.