4.3. Spline clamps and k-weight in background removal¶
4.3.1. Spline clamps¶
One of the shortcomings of the use of piece-wise splines to approximate the background function is that the ends of spline are somewhat ill-defined by virtue of not having more data preceding or following. At times, this can result in the end of the spline splaying up or down, away from the μ(E) data. This results in significant distortion to χ(k) data.
IFEFFIT provides a tool called spline clamps. These work by adding an additional term to the χ2 metric used to fit the spline to the μ(E) data. The difference between the spline and the data is computed for the first and last five data points. This sum of differences computed in energy is multiplied by a user-chosen scaling factor and added to the χ2 computed from the R-range below «rbkg». This has the effect of “clamping” the spline to the ends of the data range. In other words, we use the prior knowledge that μ0(E) is a smooth function through the oscillatory structure of μ(E) to put a restraint on the fit used to determine μ0(E).
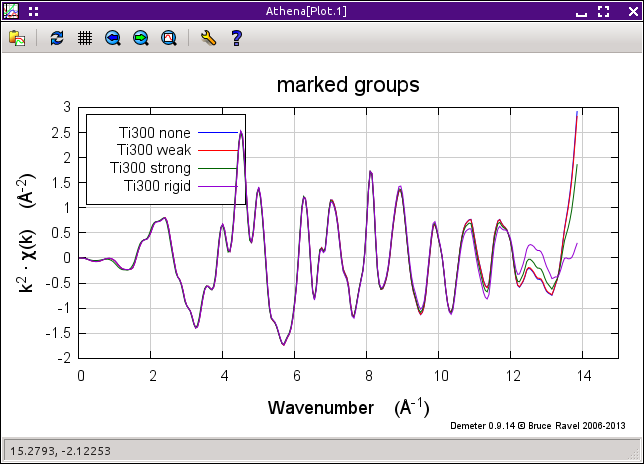
The user-selected multiplicative coefficient takes one of six predefined values: none, slight, weak, medium, strong, or rigid. These have values of 0, 3, 6, 12, 24, and 96, respectively and serve to set the strength of the clamp in the evaluation of χ2.
The default value of the clamp is none at the low end of the energy range and strong at the high end. Clamps tend not to help at the low energy end of the data. Since the μ(E) data is changing so quickly near the edge, biasing the spline to follow the data closely rarely helps improve the quality of the χ(k) data. A strong clamp at the high energy frequently improves the behavior of the spline near the end of the data.
The behavior of the clamping mechanism can be configured using the preference tool. The ♦Bkg→nclamp preference changes the number of points at the end of the data range included in the calculation of the effect of the clamp. The ♦Bkg→clamp1 and ♦Bkg→clamp2 parameters set the strengths of the two clamps. The strengths of the clamps can be fine tuned by changing the numeric values. The parameter ♦Clamp→weak sets the the weak clamp value, and so on.
4.3.2. The effect of k-weight on background removal¶
The background removal section has its own «kweight» parameter which is distinct from the k-weight used for plotting and Fourier transforms. The background removal «kweight» is the value used to evaluate the Fourier transform performed to determine the background spline. By varying the value of this «kweight», you can emphasize the lower or upper end of the data in the determination of the background.
For clean data with oscillatory structure at high energy that is small but observable, you may find that a larger value of the background removal «kweight» produces a better χ(k) spectrum. In fact, setting this parameter to 2 or 3 can have a similar impact on the data as the highest value of the spline clamp shown in the image above.
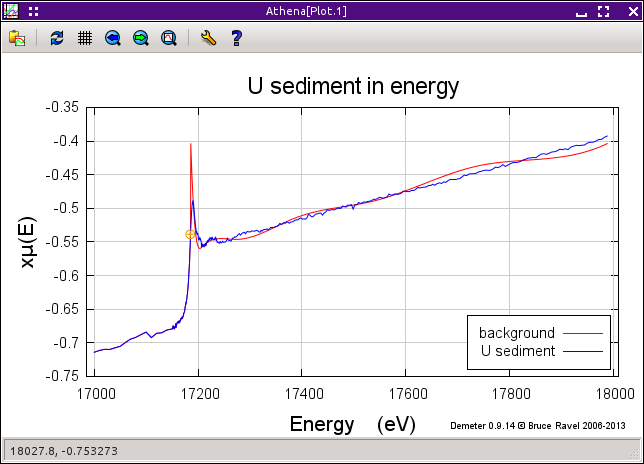
However, in data which are quite noisy, amplifying the noise by a large value of «kweight» can have a dramatic effect leading to a very poor evaluation of μ0(E). Indeed, the μ0(E) evaluated from noisy data with a large value of «kweight» will sometimes oscillate wildly, as shown in the example below.
4.3.3. The interaction between spline clamps and k-weight¶
The spline clamp and «kweight» parameters sometimes interact strongly. The criterion that μ0(E) follow closely to the end of the data that is imposed by the spline clamp can have a surprising effect on noisy, heavily k-weighted data. This is what happened in the data shown in the previous section. Reducing the strength of the spline clamp can sometimes help.
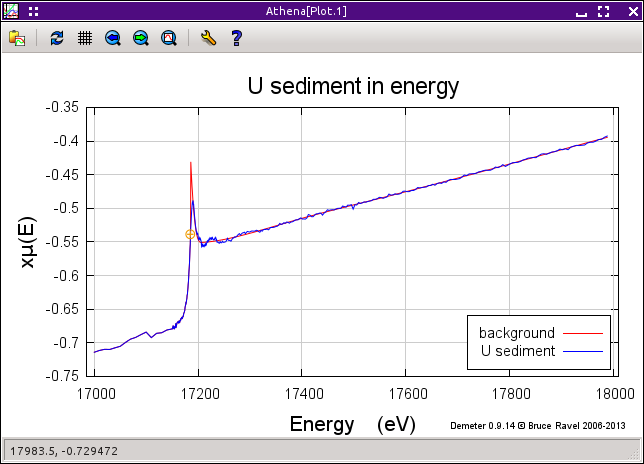
Fig. 4.24 The same noisy data as in the last figure, also with a background «kweight» of 2. However, this time the high-end spline clamp was set to none.
Sometimes your data are well served by a low «kweight» and a strong spline clamp. Other times, a large «kweight» and a weak clamp work better. Still other times, a strong «kweight» and a strong clamp work best. How do you know what to do? There are no hard and fast rules, although you will develop an intuition for how different data will respond to different parameter values. Don't be shy about trying different combinations.
DEMETER is copyright © 2009-2016 Bruce Ravel – This document is copyright © 2016 Bruce Ravel
This document is licensed under The Creative Commons Attribution-ShareAlike License.
If DEMETER and this document are useful to you, please consider supporting The Creative Commons.