Geometric parametrization of bond length
Volumetric expansion coefficient
FeS2 is a cubic crystal. Here is the crystal data
title name: Iron sulfide (pyrite)
title formula: FeS_2
title refer1: Elliot (1960) J.Chem. Phys. 33(3), 903.
space P a 3
a = 5.404
rmax = 9.00 rpath = 6.00
core = Fe
atoms
Fe 0.00000 0.00000 0.00000 Fe
S 0.38400 0.38400 0.38400 S
In this case, there are only two parameters that determine the
locations of all the atoms in the cluster – the lattice constant
a and the position of the S atom in the
unit cell. For now, we'll neglect the effect of the position of
the S atom.
In the FeS2
worked example, a parameterization was used which related ΔR
for all the paths to a volumetric expansion coefficient,
ΔR=α·Reff. Why does this work?
The distance deff between any two atoms in a cubic crystal is some
geometrical factor multiplied by the lattice constant. That factor
depends on the positions of the atoms in the unit cell, but is a pure
number.
Thus, from the FEFF calculation, deff(i, j) = ci,j·a0 for
any two atoms i and j. For any two pairs of atoms, ci,j is a
different number, but the distances between all pairs of atoms are
related by simple geometry and the value of the lattice constant.
We consider an isotropic expansion (or contraction, if α is
negative) of the unit, which is reasonable for a cubic lattice that
does not undergo a phase transition. So a = (1 + α)·a0 .
The distance between any two atoms, after accounting for the isotropic
expansion (or contraction) is
di,j = deff(i,j) + Δd(i,j)
di,j = ci,j · a
di,j = ci,j · (1+α)·a0
di,j = ci,j·a0 + ci,j·α·a0
∴ Δd(i,j) = ci,j·α·a0
Δd(i,j) = α·deff(i,j)
The expression α·deff works for all legs of any SS
or MS path in a cubic crystal (assuming that there are no internal
degrees of freedom, like the parameter for the position of the S atom
in ). The length of a path, then, is the sum of the length of
each leg. ΔR for a path is the sum of Δd for each leg.
The sum of the deff values is Reff, thus
ΔR=α·Reff.
While this trick is only valid for a cubic crystal, it does ilustrate
two important points about ARTEMIS. First, it is an example of an
interesting math expression relating a path's ΔR value to
a fitting parameter. The ΔR of the path is not itself a
variable of the fit, rather it is written in terms of α, which
is a variable of the fit.
Second, it is an example of a constraint which uses the information
content of the data very well. We can include any number of paths with
introducing new parameters for their ΔR values. α is a
robust fitting parameter in the sense that every path is involved in
its determination.
Propagating crystal distortion parameters
The room temperature structure of PbTiO3 is a tetragonal
modification of the perovskite structure. The ĉ axis is
considerably longer than the â axis. The Pb atoms lie at the
corners of the tetragonal cell, the Ti atom lies near the center of
the cell, and the O atoms lie near the centers of the faces.
In a setting which places the Pb atoms at positions of high symmetry,
i.e. right on the cell corners, the other atoms are displaced from
sites of symmetry ĉ direction. Here is the crystal data:
title PbTiO3 25C
title Glazer and Mabud, Acta Cryst. B34, 1065-1070 (1978)
core = ti Space = P 4 m m
a = 3.905 c = 4.156
rmax=3.6
atoms
! At.type x y z tag
Pb 0.0 0.0 0.0
Ti 0.5 0.5 0.539
O 0.5 0.5 0.1138 axial
O 0.0 0.5 0.6169 planar
There are 5 parameters that detrmine the positions of all the atoms in
the crystal, thus there are 5 parameters that determine the lengths of
all scattering paths. They are the two lattice constants, the
ẑ displacement of the Ti away from z=0, the ẑ displacement
of the axial oxygen atom away from z=0.5, and the ẑ displacement
of the planar oxygen atom away from z=0.5.
We set up a set of guess, def, and set parameters to encode this:
set a0 = 3.905
guess dela = 0
def a = a0 + dela
set c0 = 4.156
guess delc = 0
def c = c0 + delc
guess dti = 0.039
guess doax = 0.1138
guess dopl = 0.1169
after volume = a*a*c
 I have also defined an after parameter which computes the volume of
the unit cell. While this will not serve a purpose in the fitting
model, it is useful information to report to the log file.
I have also defined an after parameter which computes the volume of
the unit cell. While this will not serve a purpose in the fitting
model, it is useful information to report to the log file.
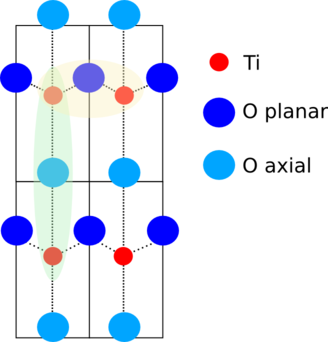
A 2-dimensional cut through this distorted perovskite is shown to the
right. The Pb atoms are above and below this plane, the
axial oxygen atoms
are in line with the
titanium atoms. The
planar oxygen atoms are
in a slightly non-collinear, buckled alignment with the Ti atoms.
The distortions of the Ti and O atoms split the first coordination
shell into three distance. Along the ẑ direction, there is a
short Ti-O distance and long one. In the buckled plane, there are
four equivalent Ti-O distances.
Computing these distances requires some simple geometry, with the
planar distance being just a bit more complicated.
def rtio_sh = (0.5 - (doax-dti)) * c
def rtio_lo = (0.5 - (doax+dti)) * c
def rtio_pl = sqrt( (a/2)^2 + ((dopl+dti)*c)^2 )
The second shell Pb atoms are similarly computed using trigonometry
and the appropriate structural parameters.
def rtipb_sh = sqrt( (a/2)^2 + c^2*(0.5 - dti)^2 )
def rtipb_lo = sqrt( (a/2)^2 + c^2*(0.5 + dti)^2 )
Finally, the Ti-Ti distances in the thrid coordination shell are
comparatively trivial. This shell is split by the tetragonal
disortion into two subshells. The distances are the lattice
constants, as you can be seen in the schematic above.
We now have math expressions for the interatomic distances between the
Ti absorber and each type of scatterer up to the third coordination
shell. These math expressions for these 7 paths are expressed in
terms of the 5 guess parameters above. The nice thing about these
expressions is that the interatomic distances are expressed in terms
of easily intepretable parameters of the crystal structure.
Now, encoding the ΔR path parameter for each of these paths is
simple. We just subtract Reff from the corresponding math
expression.
path short axial oxygen:
delr = rtio_sh - reff
path planar oxygen:
delr = rtio_pl - reff
path long axial oxygen:
delr = rtio_lo - reff
path short lead:
delr = rtipb_sh - reff
path long lead:
delr = rtipb_lo - reff
path short titanium:
delr = a - reff
path long titanium:
delr = c - reff
There are important collinear or nearly-collinear multiple scattering
paths at the distance of the third shell Ti atom. These are shown in
the yellow and green shaded areas of the schematic above.
The ΔR parameters for the axial multiple scattering paths are
simply the same as for the corresponding single scattering path. This
is the case because the distortions in PbTiO3 are all in the
ẑ direction, so those MS paths must have the same length as the
corresponding SS paths.
In the planar direction, you need to add up the lengths of the legs
and subtract Reff for their ΔR parameters:
path planar double scattering:
delr = (a + 2*rtio_pl)/2 - reff
path planar triple scattering:
delr = 2*rtio_pl - reff
This strategy of adding up leg lengths works for any kind of multiple
scattering path you include in this fit.
This is lovely! With 5 guess parameters and some well-considered
math expressions, we are able to encode ΔR parameters for all
the paths in the fit. As more scattering paths are considered for the
fit, it is not necessary to include any more guess parameters for
ΔR.
Parametrizations of distance in non-crystalline materials
Interesting geometrical constraints on distance are not the sole
province of crystalline materials. In the following two papers, I
show the details of an analysis of Hg bound to the pyrimidine ring of
a nucleotide in a synthetic DNA structure. To cope with severe
information limits in my data, I made some simplifying assumptions
about the structure of the Hg/DNA complex. I then employed a bit of
trigonometry to express all the absorber-scatterer distances as
functions of a small number of guess parameters.
 Need more examples
Need more examples
| ![[Artemis logo]](../../images/Artemis_logo.jpg)

 Need more examples
Need more examples