13.2. Example 2: Methyltin¶
Some years ago, some colleagues from the U.S. Environmental Protection Agency came to me with an interesting problem about the fate and transport of organic tin compounds through sewage systems. In the U.S. (and elsewhere), municipal water is carried into homes and office buildings with copper pipes and waste water is transported to the water treatment system in polyvinyl chloride (PVC) pipes. By itself, PVC is a highly malleable plastic. Like many plastics, it is made stiff by the addition of stiffening agents added to the plastic matrix. In the case of PVC, organic tin compounds are used.
The folks from the EPA were studying the accumulation of tin in municipal waste and trying to understand if there was a mechanism of transport involving leaching from PVC pipes. We made a series of XAS measurements on various organic tin standards as well as direct measurement of PVC pipes produced by three different manufacturers.
- Christopher A. Impellitteri, Otis Evans, and Bruce Ravel. Speciation of organotins in polyvinyl chloride pipe via X-ray absorption spectroscopy and in leachates using GC-PFPD after derivatisation. J. Environ. Monit., 9:358–365, 2007. doi:10.1039/B617711E.
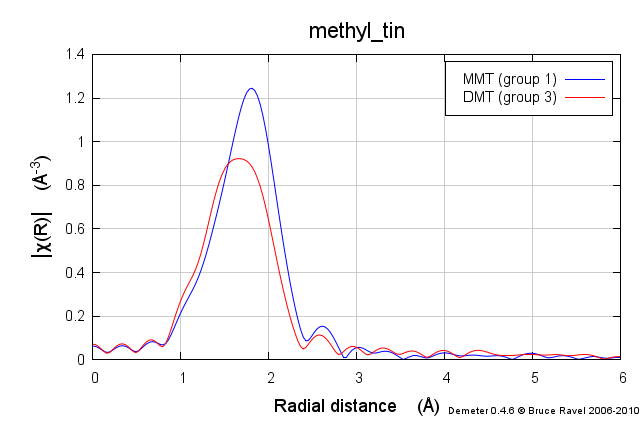
Two of the standard compounds we measured were methyltin chloride, as shown below.
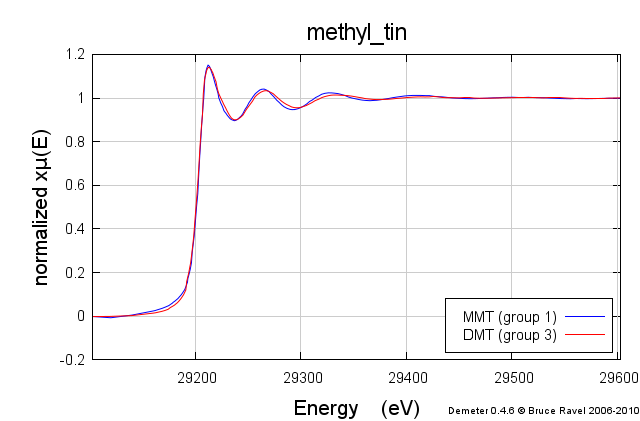
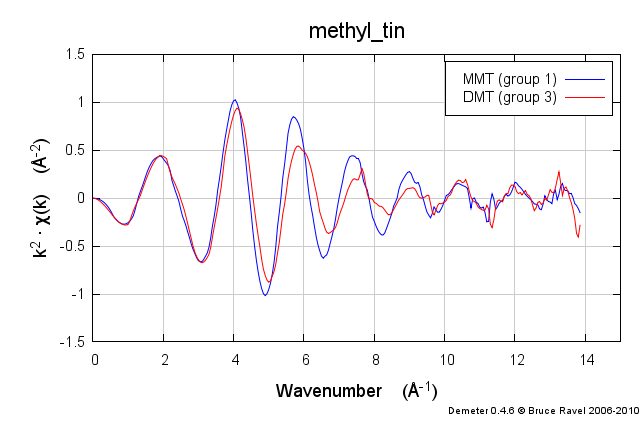
These samples were prepared in solution. This solution was packed into a simple transmission sample cell for liquids. Transmission EXAFS were measured. Here is the data:
These data are quite similar, but there is a distinct change in the χ(R) spectrum between the two.
In this section, we will step through the corefinement of these two data steps, creating a constrained fitting model that uses the information content of both data sets to allows excellent measurement of a number of structural parameters.
You can find example EXAFS data and a structure from which to build
the feff.inp file at my XAS Education site.
Import the μ(E) data into ATHENA. When you are content
with the processing of the data, save an ATHENA project
file and dive into this example.
13.2.1. Import data¶
After starting ARTEMIS,  click on the
Add button at the top of the Data sets
list in the Main window. This will open a file selection dialog.
Click to find the ATHENA project file containing the data
you want to analyze. Opening that project file displays the project
selection dialog.
click on the
Add button at the top of the Data sets
list in the Main window. This will open a file selection dialog.
Click to find the ATHENA project file containing the data
you want to analyze. Opening that project file displays the project
selection dialog.
The project file used here has the data from both methyltin standards. Select “Dimethyl Tin” from the list. That data set gets plotted when selected.
Now  click the Import button. That
data set gets imported into ARTEMIS. An entry for the
dimethyl tin is created in the Data list, a window for interacting
with the dimethyl tin data is created, and the dimethyl tin data are
plotted as χ(k).
click the Import button. That
data set gets imported into ARTEMIS. An entry for the
dimethyl tin is created in the Data list, a window for interacting
with the dimethyl tin data is created, and the dimethyl tin data are
plotted as χ(k).
The next step is to import some structural data that can be used to
make the FEFF calculation. Since this is a solution
standard, there is obviously not an atoms.inp file. So we
need to find another way to create the feff.inp file.
A bit of searching on Google eventually turned up the following structural information for dimethyltin dichloride in the form of a Protein Data Bank file. PDB is a format that is usually used to store structural data for large macromolecules, but is also quite suitable to tiny molecules like our methyl tin sample. This example has some chaff that is not of interest to us for our EXAFS analysis problem, but among the chaff is all the information we need.
COMPND 5261536
HETATM 1 C1 LIG 1 -0.027 2.146 0.014 1.00 0.00
HETATM 2 SN2 LIG 1 0.002 -0.004 0.002 1.00 0.00
HETATM 3 C3 LIG 1 1.042 -0.716 1.744 1.00 0.00
HETATM 4 CL4 LIG 1 -2.212 -0.821 0.019 1.00 0.00
HETATM 5 CL5 LIG 1 1.107 -0.765 -1.940 1.00 0.00
HETATM 6 1H1 LIG 1 0.996 2.523 0.006 1.00 0.00
HETATM 7 2H1 LIG 1 -0.554 2.507 -0.869 1.00 0.00
HETATM 8 3H1 LIG 1 -0.537 2.497 0.911 1.00 0.00
HETATM 9 1H3 LIG 1 0.532 -0.365 2.641 1.00 0.00
HETATM 10 2H3 LIG 1 1.057 -1.806 1.738 1.00 0.00
HETATM 11 3H3 LIG 1 2.065 -0.339 1.736 1.00 0.00
END
Note that columns 6, 7, and 8 contain the Cartesian coordinates of the tin, chlorine, carbon, and hydrogen atoms that make up the dimethyltin dichloride molecule. The third column identifies which atomic species lives at each of the sites. Perfect!
A bit of cutting and pasting into en empty template for a
feff.inp file, resulted in the following:
TITLE dimethyltin dichloride
HOLE 1 1.0 * Sn K edge (29200.0 eV), second number is S0^2
* mphase,mpath,mfeff,mchi
CONTROL 1 1 1 1
PRINT 1 0 0 0
RMAX 6.0
*CRITERIA curved plane
*DEBYE temp debye-temp
NLEG 4
POTENTIALS
* ipot Z element
0 50 Sn
1 17 Cl
2 6 C
3 1 H
ATOMS
* x y z ipot tag distance
-0.027 2.146 0.014 2
0.002 -0.004 0.002 0
1.042 -0.716 1.744 2
-2.212 -0.821 0.019 1
1.107 -0.765 -1.940 1
0.996 2.523 0.006 3
-0.554 2.507 -0.869 3
-0.537 2.497 0.911 3
0.532 -0.365 2.641 3
1.057 -1.806 1.738 3
2.065 -0.339 1.736 3
This was saved to disk, then imported into ARTEMIS by
 left clicking on the line in the Data window that
says Import crystal data or a Feff calculation, then
selecting our
left clicking on the line in the Data window that
says Import crystal data or a Feff calculation, then
selecting our feff.inp file from the column selection dialog.
With the methyltin structural data imported, run FEFF by
 clicking the Run Feff button
to compute the scattering potentials and to run the pathfinder.
clicking the Run Feff button
to compute the scattering potentials and to run the pathfinder.
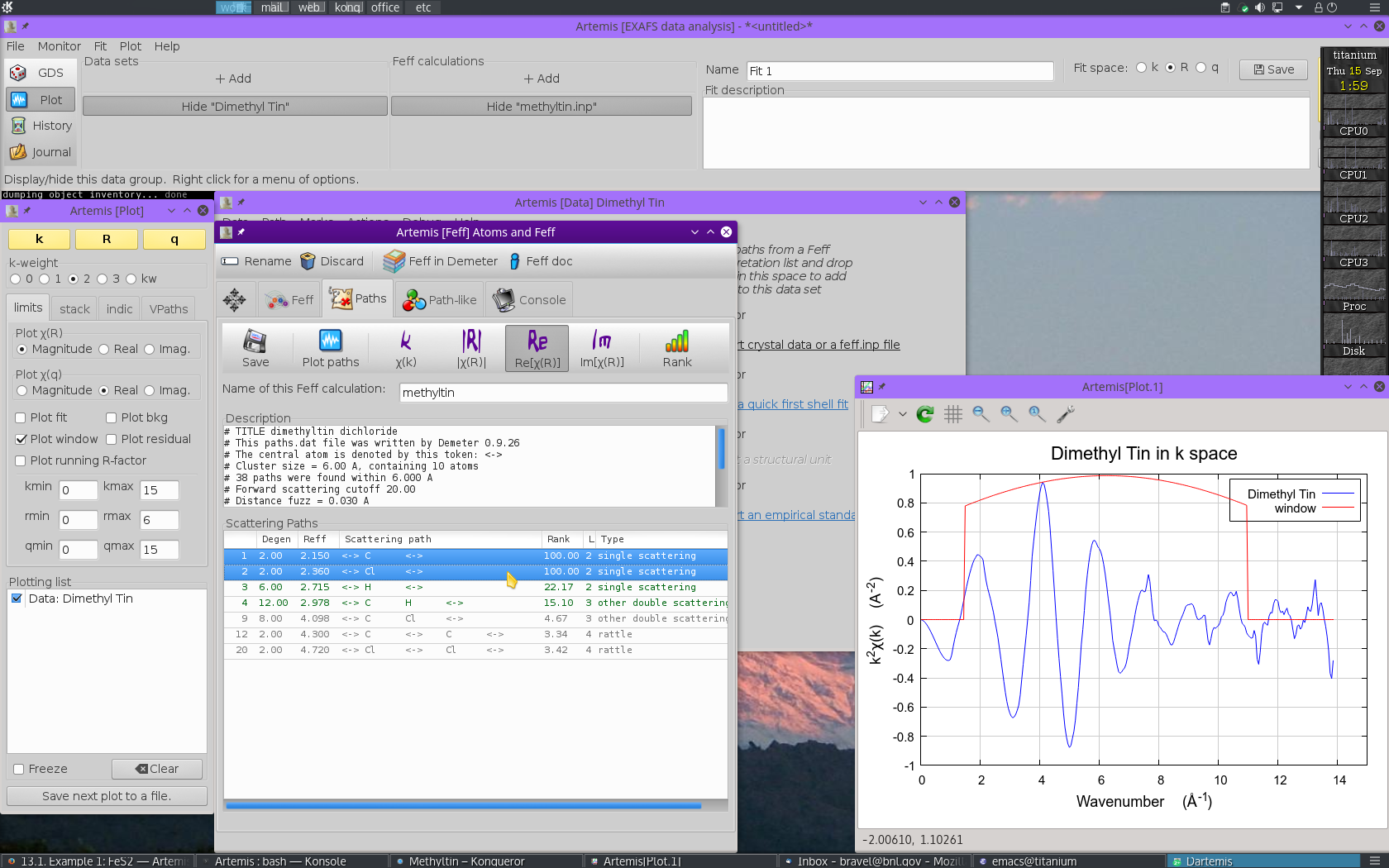
Once the FEFF calculation is finished, the path
intepretation list is shown in the Paths tab. This is the list of
scattering paths, sorted by increasing path length. Select the first
2 paths by  clicking on the path
0000, then Control-
clicking on the path
0000, then Control- clicking
on path 0002. The selected paths will be highlighted.
clicking
on path 0002. The selected paths will be highlighted.
 Click on one of the highlighted paths and,
without letting go of the mouse button,
Click on one of the highlighted paths and,
without letting go of the mouse button,  drag the paths
over to the Data window and drop them onto the empty Path list.
drag the paths
over to the Data window and drop them onto the empty Path list.
 Dropping the paths on the Path list will associate
those paths with that data set. That is, that group of paths is now
available to be used in the fitting model for understanding the
methyltin data.
Dropping the paths on the Path list will associate
those paths with that data set. That is, that group of paths is now
available to be used in the fitting model for understanding the
methyltin data.
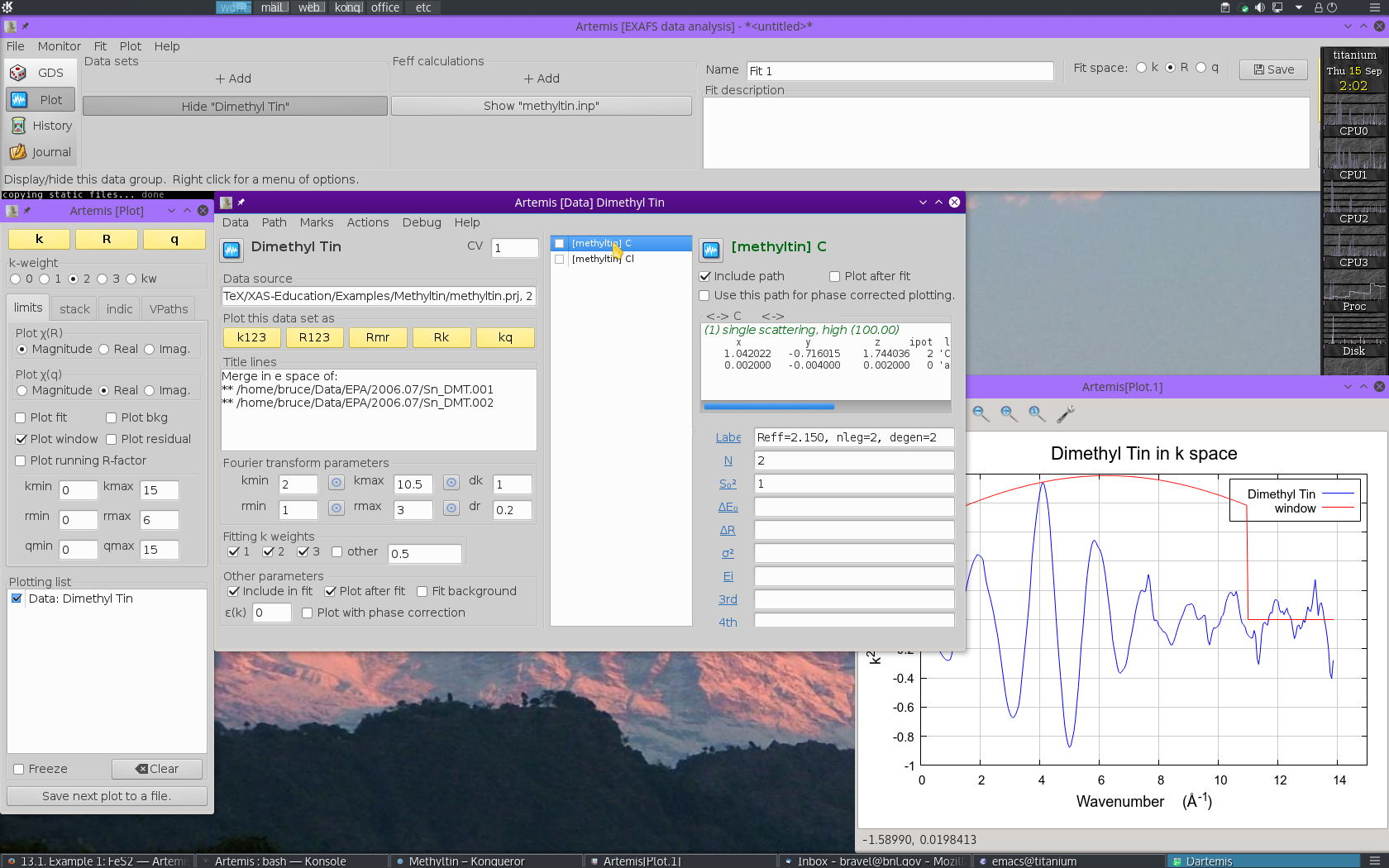
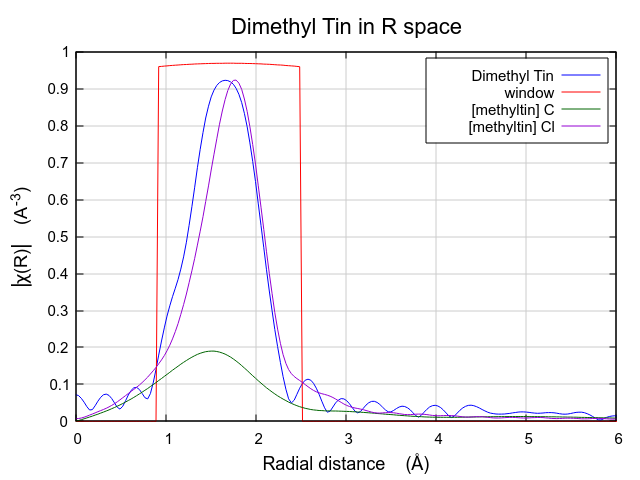
Each path will get its own Path page. The Path page for a path is displayed when that path is clicked upon in the Path list. Shown below is the dimethyltin dichloride data with 2 paths. The first path in the list, the one representing the contribution to the EXAFS from the C single scattering path nominally at 2.150 Å, is currently displayed. The second path represents the contribution to the EXAFS from the Cl single scattering path nominally at 2.360 Å.
13.2.2. Examine the scattering paths¶
The first chore is to understand how these two paths from the FEFF calculation relate to the data. To this end, we need to populate the Plotting list with data and paths and make some plots.
Mark single scattring paths for the C and Cl by  clicking on their check buttons. Transfer those two paths to the
Plotting list by selecting .
clicking on their check buttons. Transfer those two paths to the
Plotting list by selecting .
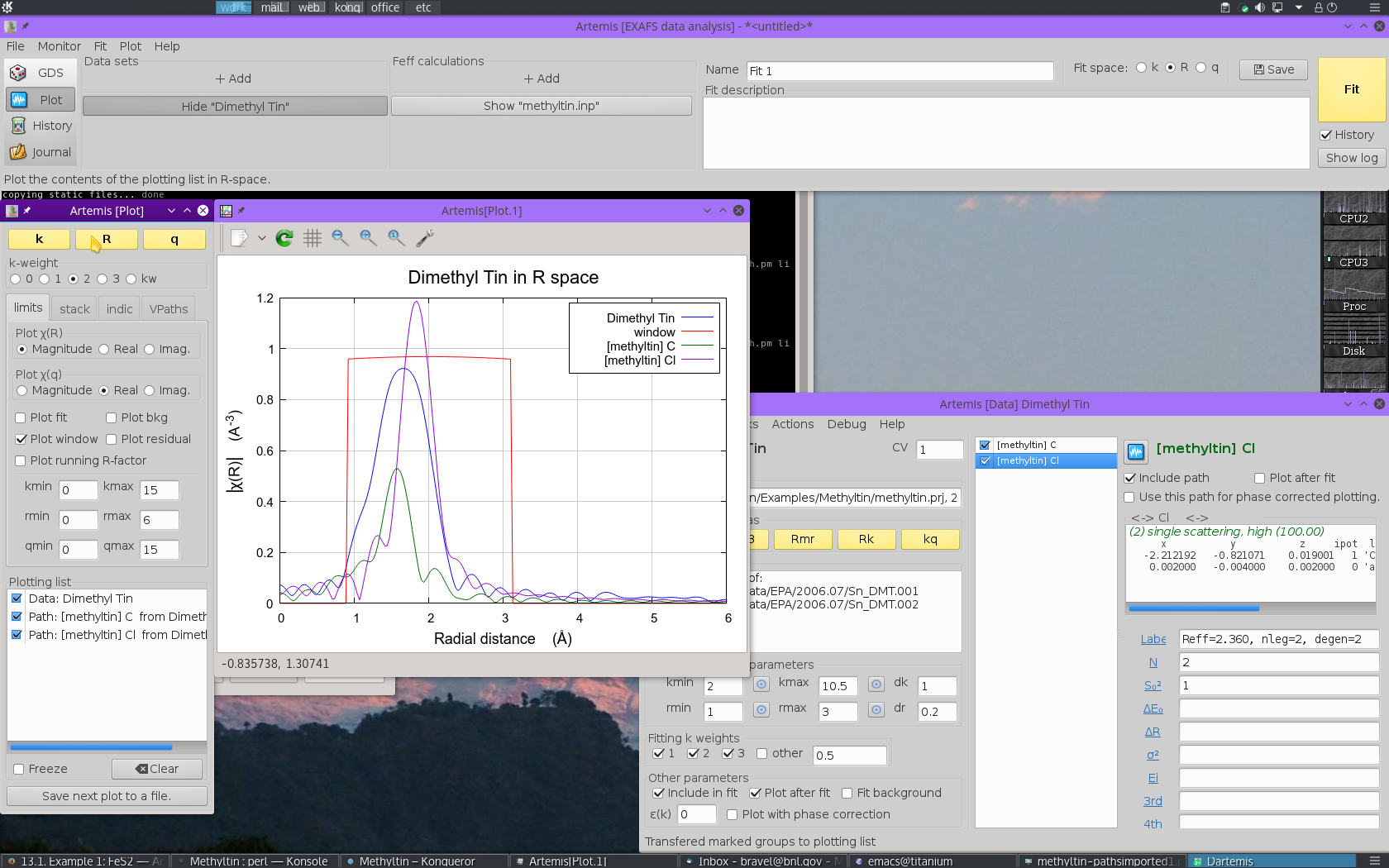
With the Plotting list poluated as shown below,  click on the R plot button in the Plot window to make
the plot shown.
click on the R plot button in the Plot window to make
the plot shown.
These two paths reasonably might represent the peak in the dimethyltin
dichloride data, although it is not clear how the lower part of that
peak will be represented by these two paths. It is instructive also
to look at the data as the real part of the Fourier transform. To do
so,  click the Real radiobutton under
Plotχ(R) in the Plotting window. This
will display the following plot:
click the Real radiobutton under
Plotχ(R) in the Plotting window. This
will display the following plot:
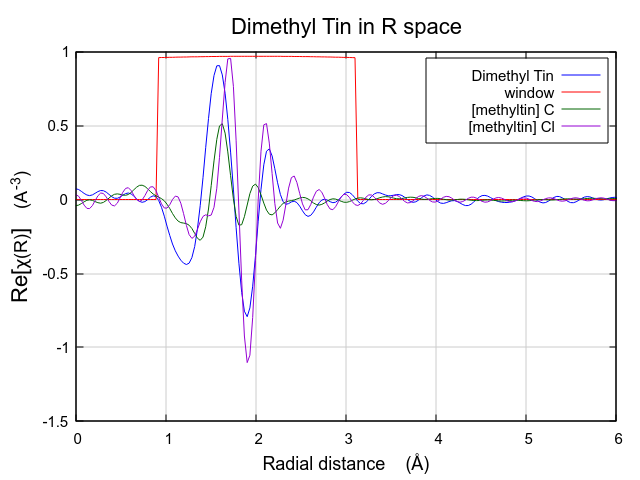
Viewed this way, it is clear that this FEFF calculation is likely to do a good job fitting these data. The missing spectral weight at low R could likely be recovered by a ΔR shift of the the C scatterer to lower R.
13.2.3. Fit to the dimethyltin dichloride data¶
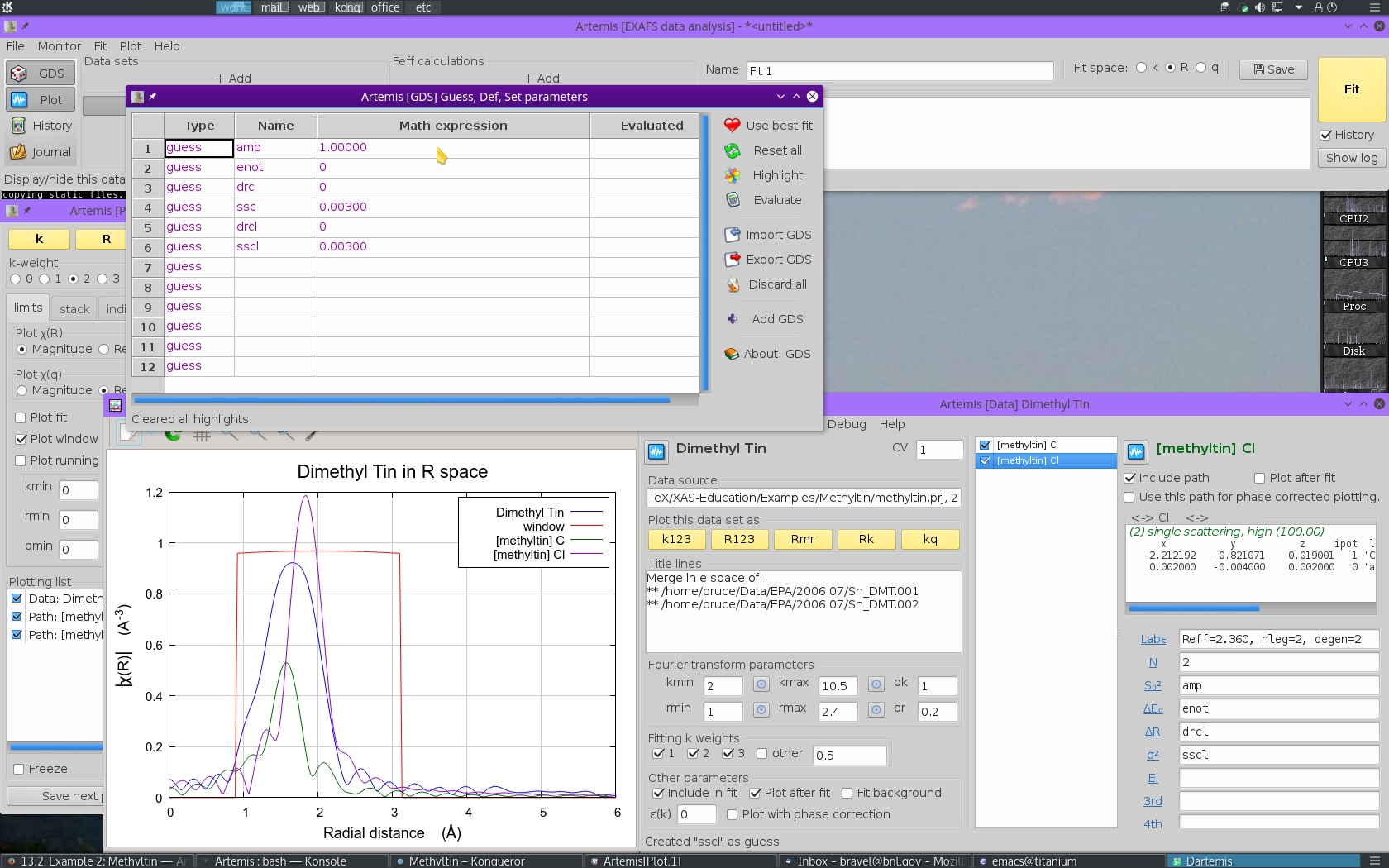
As in many fits, we will use a single parameter to represent the S20 for each path. This is reasonable as this is a parameter of the absorber and we are making only one FEFF calculation in this fit. For the same reason, we will use a single E0 parameter for each path. We don't have any a priori knowledge of how the Sn-C and Sn-Cl bonds might be related. As a result, we will float independent ΔR and σ2 for the two ligands. This results in 6 fitting parameters.
- Make sure both the C and Cl paths are included in the fit. That is, each should have its Include path button checked.
- Set the values of Rmin and Rmax to cover just the first peak. 1 Å to 2.4 Å is a good choice.
- We need parameters to represent S20 and E0. The parameters
ampandenotare defined in the GDS window and given sensible initial guess values. - We need ΔR and σ2 for each ligand type.
The ΔR parameters are called
drcanddrcl. The σ2 are calledsscandsscl.
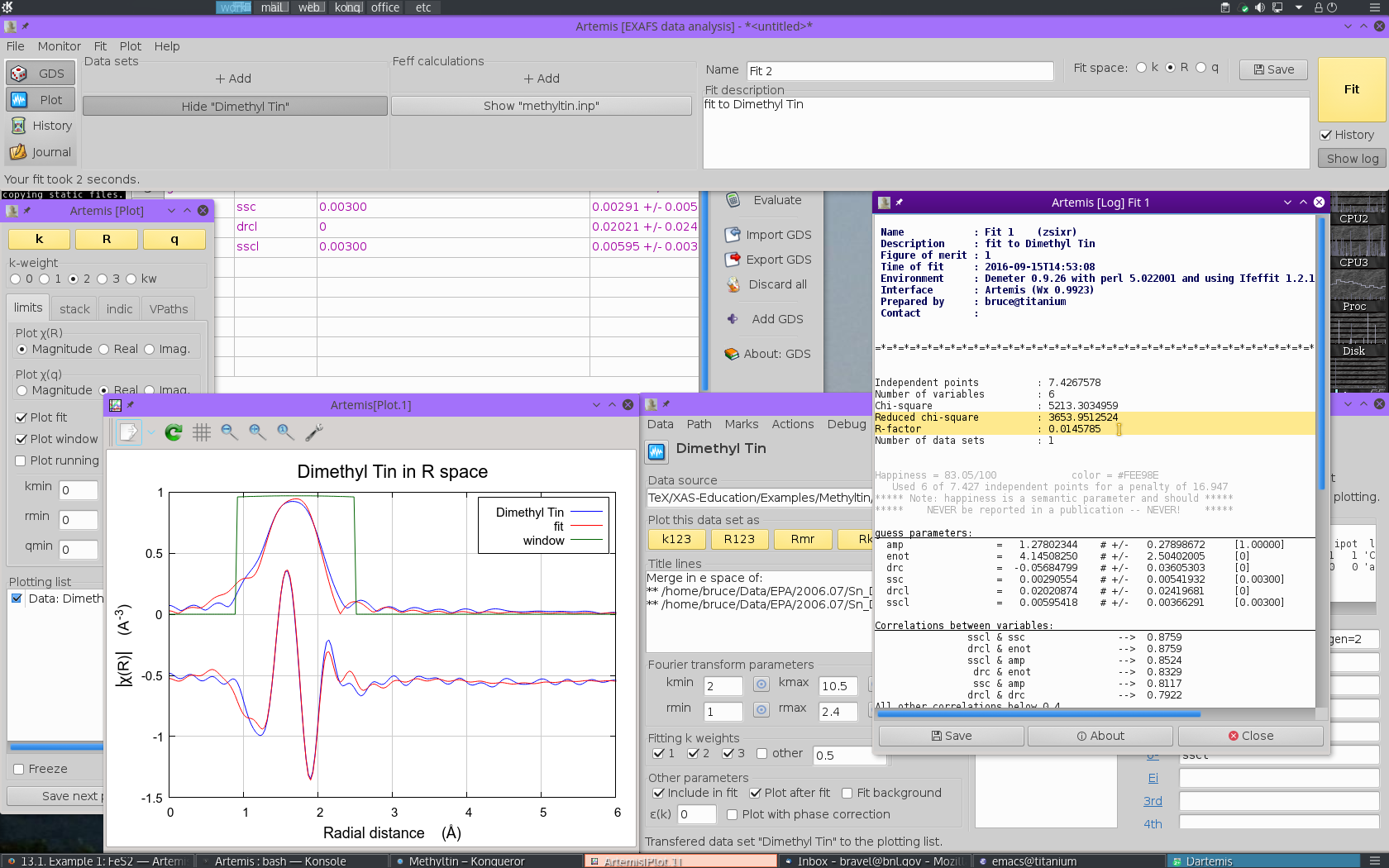
At this point we are ready to  click the big fit
button. Doing so yields the following:
click the big fit
button. Doing so yields the following:
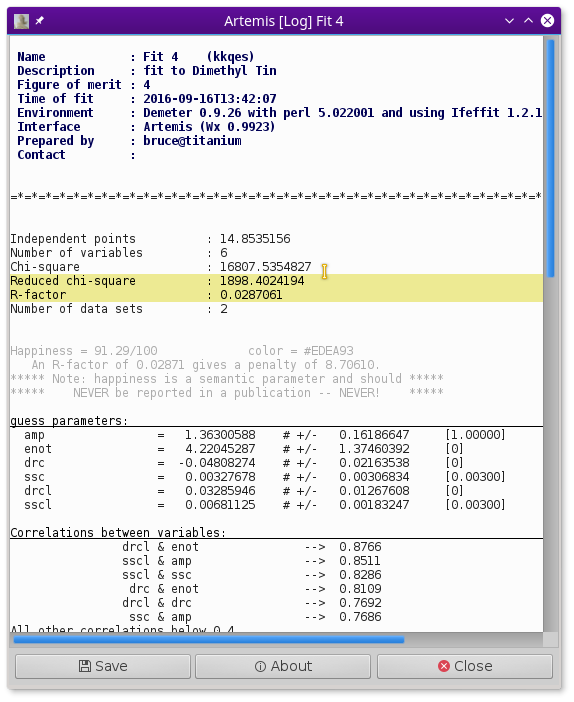
Glancing at the plot window, this looks like a decent enough fit. Examining the log file, we find that the fit is fairly well interpretable.
- The S20 value is 1.27±0.28, which is rather larger than expected
- E0 is 4.1±2.5 eV, a reasonable value which suggests that E0 was chosen reasonably in ATHENA.
- As expected, ΔR for the C ligand is negative and fairly large at -0.057±0.036 Å. The ΔR for the Cl ligand is positive, but consistent with zero, 0.020±0.024 Å.
- Both σ2 values are of a reasonable size, 0.00291±0.00542 Å2 for C and 0.00595±0.00366 Å2 for Cl.
Note, however, that the information content of this fit is being heavily strained. With a k-range of 2 Å-1 to 10.5 Å-1 and an R-range of 1 Å to 2.4 Å, there are only about 7.4 independent measurements in these data. The six parameters floated in this fit are a significant burden on these data.
13.2.4. The benefit of multiple k-weight fitting¶
Before extending this fitting project to consider corefinement of the two methyltin data sets, let us pause and consider the merits of multiple k-weight fitting.
The default in ARTEMIS is to perform the fit with k-weighting of 1, 2, and 3. The implementation of this is quite simple. The normal χ2 fitting metric is evaluated for each value of k-weighting considered. The sum of all these χ2 evaluations is then minimized to produce the fit. The advantage of doing this can be seen when considering the impact of the various path parameters on the EXAFS equation.
A σ2 parameter is always multiplied by k2 in the EXAFS equation. Thus the portion of the fitting metric evaluated at high k is much more sensitive to a poorly chosen value of σ2 than the portion evaluated at low k. Since a k-weighting of 3 amplifies the value of the data (and theory) more and more as k increases, evaluating the fit with a k-weight of 3 will provide more sensitivity to σ2 parameters. The other amplitude parameter, S20, affects all regions of the k-range equally.
Similarly, ΔR is multiplied by k in the EXAFS equation, thus the evaluation of the fitting metric at high k is much more sensitive to a poorly chosen value. E0, on the other hand, has a much bigger impact on the evaluation of the fitting metric at low k. Thus a k-weight of 3 will provide greater sensitivity to ΔR in the fit while a k-weight of 1 will provide a greater sensitivity to E0.
One might think, then, that a k-weight of 2 would be a good compromise between the demands of the various parameters. Let's check that out.
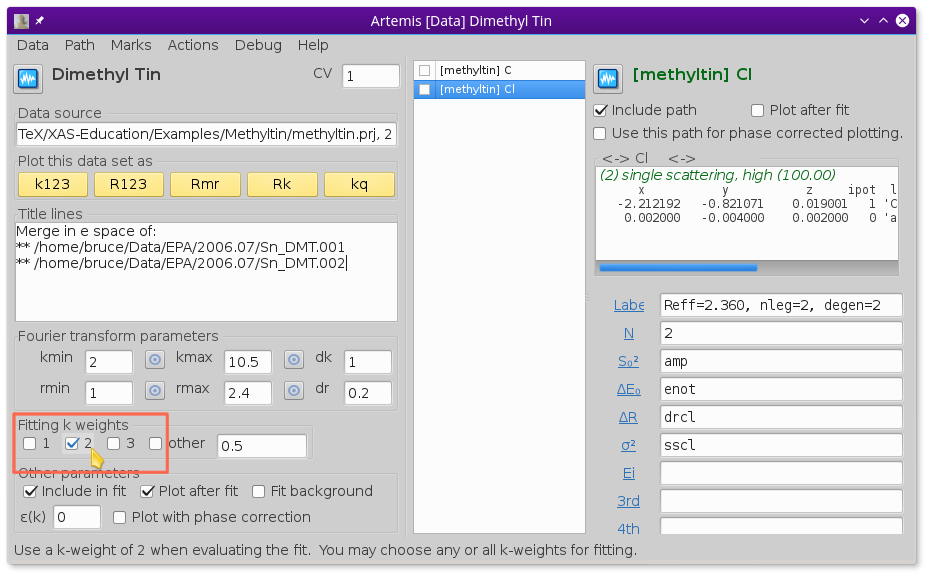
To perform a fit with just k-weight of 2,  unclick
the 1 and 3 buttons as shown in
Fig. 13.28.
unclick
the 1 and 3 buttons as shown in
Fig. 13.28.
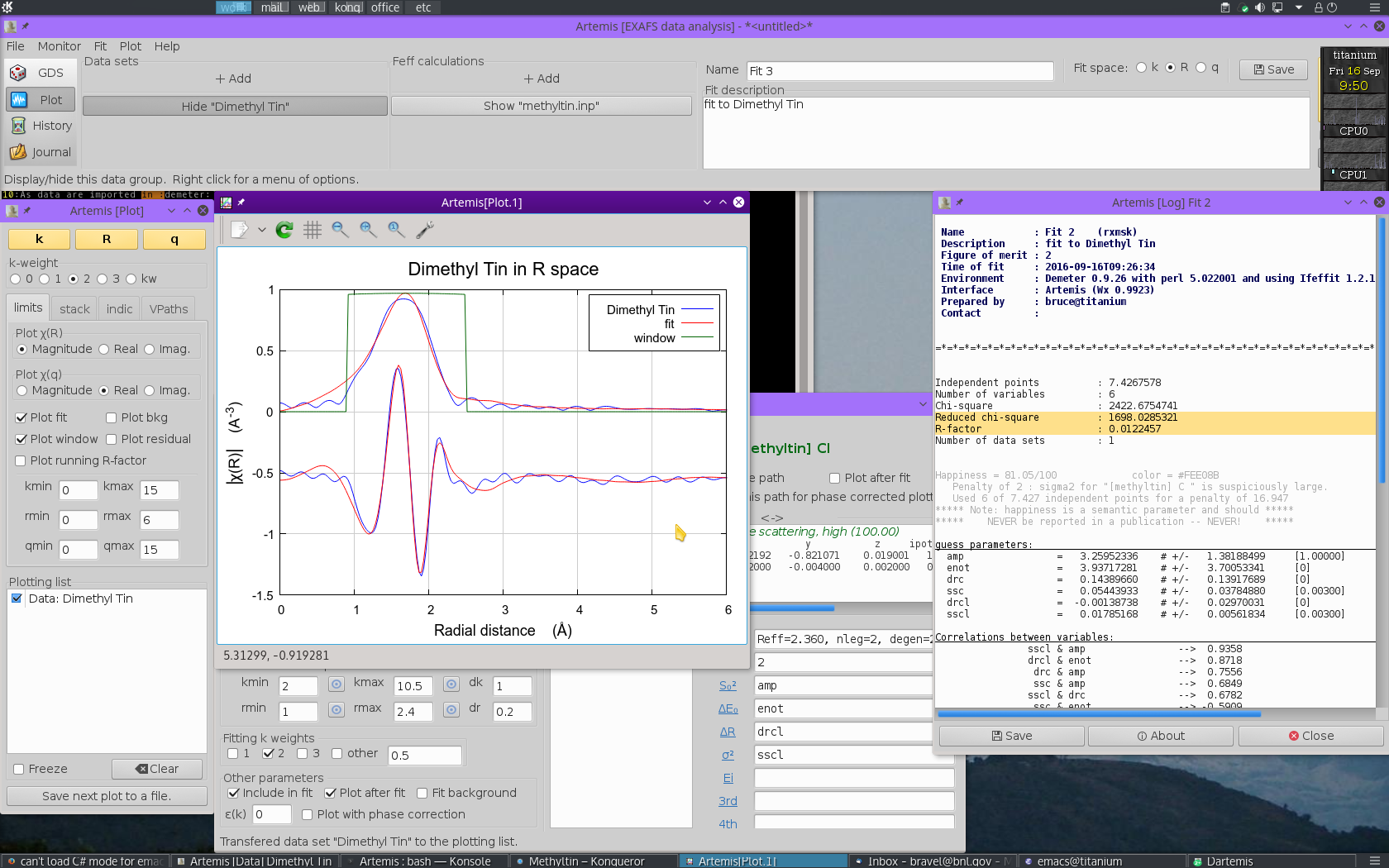
We  click the big fit button and a minute later we
see this:
click the big fit button and a minute later we
see this:
On the surface, this appears to be a comparable fit to the one made with multiple k-weighting. The quality of the plot is similar, as is the value of R-factor. Closer examination of the fitting parameters turns up a number of serious problems.
- The value of S20 is 3.26±1.38! The result with multiple k-weight fitting was also greater than 1, but could possibly be explained as a problem of sample preparation or mean free path. This value is just nonphysically enormous.
- To compensate for the large S20, the values for σ2 are also unreasonably large, 0.05444±0.03785 Å2 for C and 0.01785±0.00562 Å2 for Cl.
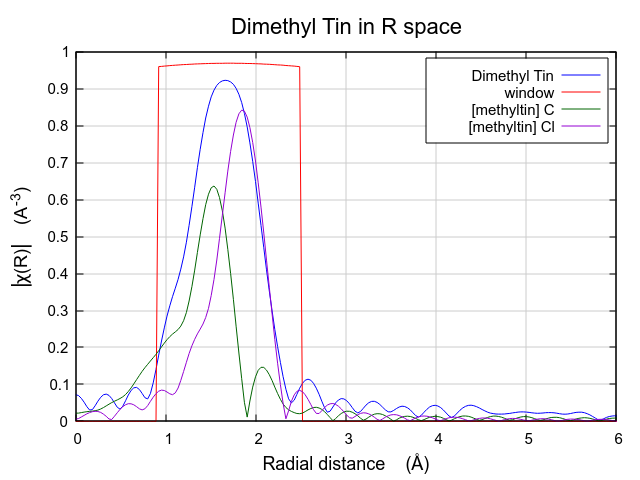
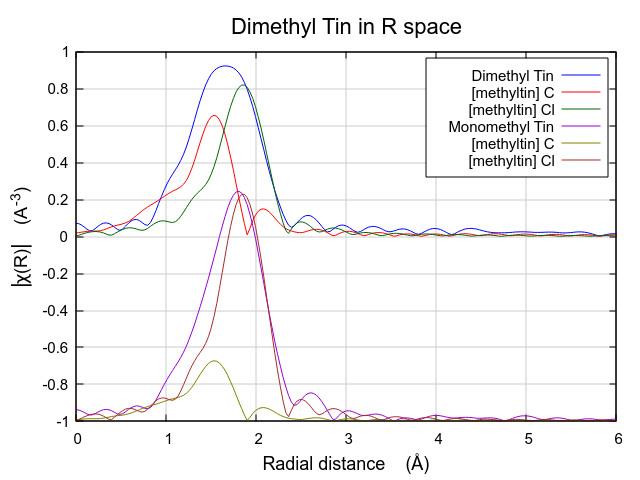
The effect of these hard-to-understand values for S20 and σ2 can be seen in Fig. 13.31. Both contributions are very broad, as expected given their large values for σ2. This is in contrast to the contributions from the multiple k-weight fit shown in Fig. 13.30, where they are of a width that seems more reasonable for tightly bound ligands.
In this situation, where the number of guess parameters is such a large fraction of the total information content of the data, the use of multiple k-weight fitting is essential. The added sensitivity to the various regions of k-space afforded by the evaluation of the fitting metric with different k-weight values helps reduce the very high correlations between the S20 and σ2 parameters, resulting in a much more defensible fit.
13.2.5. Corefining multiple data sets¶
The solution to the problem of the number of guess parameters being so close to the number of independent points is to expand the bandwidth of the data. This is often done by extending the fitting model to include higher coordination shells, then importing and parameterizing additional FEFF paths to account for the structure at higher R. In this case, that will not work. These data have very little structure beyond about 2.5 Å. In this case, what we have fit so far is all there is to the data.
Another way of increasing the information content is to corefine multiple data sets. Adding a second data can double the information content of the fitting model. If the fitting model can be made to accommodate the new data set without doubling the number of guess parameters, the model should be more robust.
In this case, we will double the information content by adding the monomethyltin trichloride to the project – both methyltin data sets were measured over the same k-range and consist of a single peak in R. If we assume that the sate of the Sn atom is the same in both materials and we take care to align the data well in ATHENA, then we will not need to introduce new parameters for S20 or E0.
If we further assume that the nature of the Sn-C and Sn-Cl bonds are very similar in the two forms of methyltin, then we can reuse the ΔR and σ2 parameters for the C and Cl scatterers.
Thus we can double the information content of the fit while adding no new parameters!
To start, use the file selection dialog to again open the ATHENA project file containing the methyltin data. Select the monomethyltin data. This will import the second data set, add it to the Data sets list in the main window, and create a Data window for monomethyltin. All of this is shown in Fig. 13.32.
Re-open the window containing the FEFF calculation, then
 drag and drop the same two paths onto the
monomethyltin window.
drag and drop the same two paths onto the
monomethyltin window.
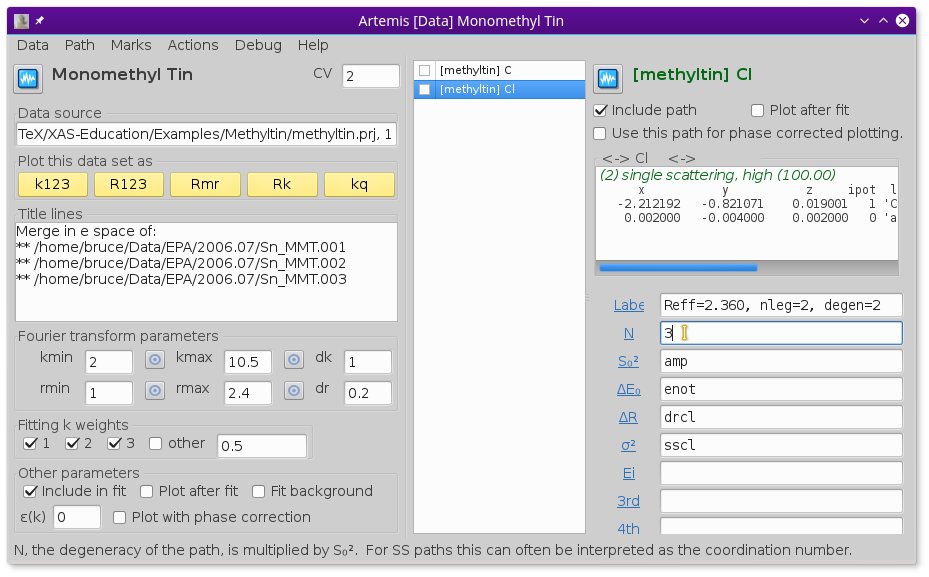
Fig. 13.33 Reuse the guess parameters from before, but change the coordination numbers for C and Cl to 1 and 3, respectively.
Edit the path parameters so that the paths in the new monomethyltin window use the same parameters for S20, E0, ΔR, and σ2 as were used for the dimethyltin.
To account for the different numbers of C and Cl ligands, the N path parameters must be changed to 1 for C in the dimethyltin data window and 3 for the Cl.
Make sure the R-range is set sensibly. You are now ready to hit the big fit button.
This is a decent fit. The guess parameters are mostly reasonable, although the S20 parameter is still somewhat large. E0, ΔR, and σ2 values are all defensible. The uncertainties on most of the parameters are smaller than in earlier fits. Most importantly, we are not stressing the information content of the data so severely by fitting 6 parameters.
My having more unused information available, we can explore other possibilities in these data that would not have been possible in the single data set fit. For example, we could examine the impact of the H single scattering paths on the fit or we could try lifting the constrains on the ΔR and σ2 parameters of the two ligand types.
13.2.6. Further exploration¶
- Could the Fourier transform range be longer? Look at the k123 plot for each data set.
- Could the fitting range be longer? Well, there is not much signal beyond the first shell above the noise level. Simply expanding the R-range to make Nidp larger without actually including signal is cheating.
- Is the assumption about the bonds in the two samples valid? How would you go about testing that assumption?
- Trimethyltin monochloride would have been a useful measurement....
- The ΔRs for both Sn-C and the Sn-Cl are somewhat large.
The fit might be improved by adjusting the original
feff.inp, re-running FEFF, and re-doing the fit. - The structure used in the FEFF calculation is unbounded from the outside, which might effect the construction of muffin tins. Packing water molecules around the DMT molecule might help.
- Is the dimethyltin feff calculation really transferable to monomethyltin? You could test this by finding or creating a structure for monomethyltin trichloride and running FEFF on that.
DEMETER is copyright © 2009-2016 Bruce Ravel – This document is copyright © 2016 Bruce Ravel
This document is licensed under The Creative Commons Attribution-ShareAlike License.
If DEMETER and this document are useful to you, please consider supporting The Creative Commons.